旋转曲面

一条平面曲线绕平面上一条直线旋转
考得多的就是曲线绕坐标轴旋转的旋转面方程，如果更一般的，绕着旋转的直线轴是空间中的任意直线，应该怎么算呢

曲线 绕一条定直线旋转一周所形成的曲面
曲线 绕直线 旋转一周形成一个旋转曲面, 旋转曲面方程的求法如下：
这里对于直线方程要用的最重要的两个要素，点和方向向量
而在曲线上我们要设一个点出来

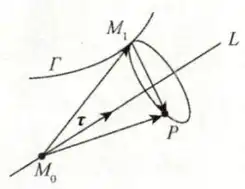
设 ,方向向量 . 在母线 上任取一点 ,则过 的纬圆上的任意一点 满足条件

对于这里 的理解

既然是曲线绕着轴转，肯定这个轴是垂直于这个绕出来的平面的，要是都不垂直，可以自己用手指拿出来绕一绕，会发现，这个绕出来的平面压根就没法闭合封闭起来

对于这两个方程，用坐标的方式写表达，有

这两个方程和，表达曲线的两个曲面方程, 和 继续联立，便可得到旋转曲面的方程，我们目标是始终是要消元只保留设出来的

按照这个逻辑，给出绕坐标轴旋转的旋转面方程的推导过程
常考曲线 绕 轴旋转一周而成的旋转曲面的方程.

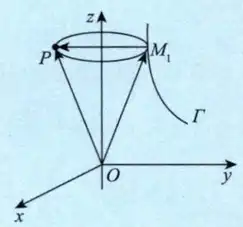
图 17-2
如图 17-2 所示，在曲线 上任取一点 ,则过点 的纬圆上的任意一点 满足条件 和 ,即 且 ,得

从方程组 中消去 和 ,便得到旋转曲面的方程.
如果能从方程组 中解出 和 ,则旋转曲面的方程为

如求 绕 轴旋转一周而成的旋转曲面的方程,由方程组知 则旋转曲面的方程为 ,即 .