题18
题目
[!question]+
(18) (本题满分 10 分)设函数
分析
[!NOTE]+
应该是把
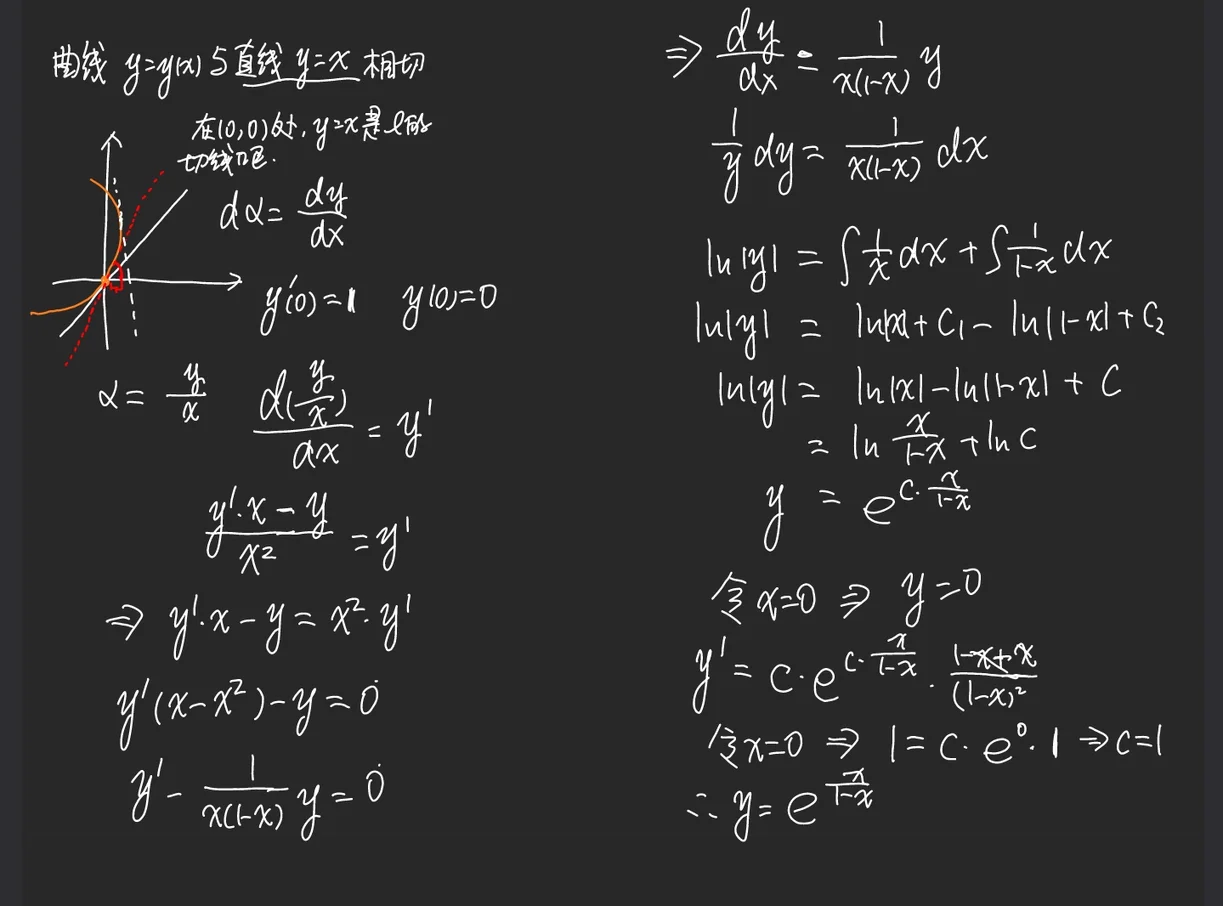
解
[!done]-
解 (法一) 构造关于
由
由导数的几何意义知,
由于曲线
下面求
由于
因此,
Jun 19, 20253 min read
[!question]+
(18) (本题满分 10 分)设函数
[!NOTE]+
应该是把
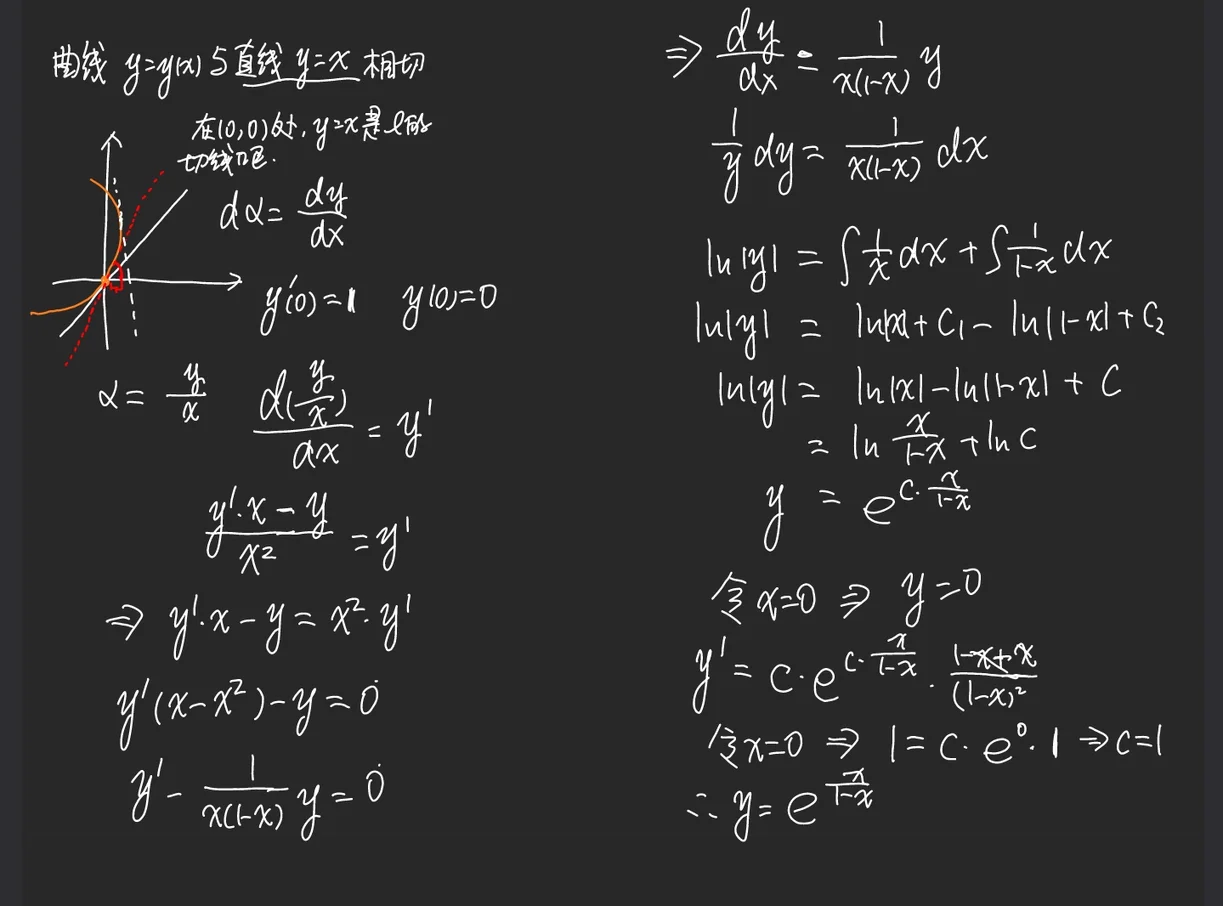
[!done]-
解 (法一) 构造关于
由
由导数的几何意义知,
由于曲线
下面求
由于
因此,