题18
题目
[!question]+
计算二重积分
分析
[!NOTE]+


解
[!done]-
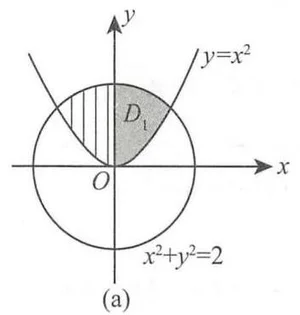
解 由图 (a) 可知,区域
其中
(b) (c)
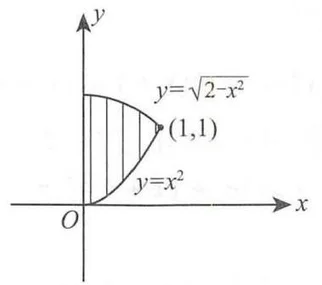
(法一) 在直角坐标系下计算.
如图(b) 所示,先求出圆弧
由圆方程
从而
因此,
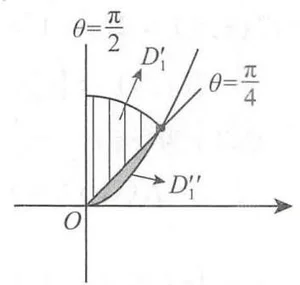
(法二) 在极坐标系下计算.
写出
可求得圆弧与抛物线的交点坐标为
因此,
Jun 19, 20254 min read
[!question]+
计算二重积分
[!NOTE]+


[!done]-
解 由图 (a) 可知,区域
其中



(b) (c)
(法一) 在直角坐标系下计算.
如图(b) 所示,先求出圆弧
由圆方程
从而
因此,
(法二) 在极坐标系下计算.
写出
可求得圆弧与抛物线的交点坐标为
因此,