题14

题14

题目

一棵二叉树的先序遍历序列为 1234567 ，它的中序遍历序列可能是 ( ).
A. 3124567
B. 1234567
C. 4135627
D. 1463572

分析

只知道先序的问题是，不知道左右子树到底有多长
可以试选项来这么做，因为先序遍历和中序遍历可以唯一确定树

解

B


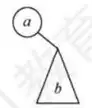
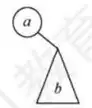
(c)

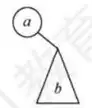
(d)

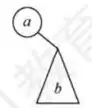
(e)

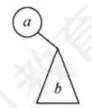
解法 1: 由题可知, 1 为根结点, 2 为 1 的孩子。对于 A, 3 应为 1 的左孩子, 前序序列应为 ,不符题意。类似的, 也错误。
对于 为 1 的右孩子,3 为 2 的右孩子……满足题意。 对于 D, 463572 应为 1 的右子树, 2 为 1 的右孩子, 46357 为 2 的左子树, 3 为 2 的左孩子, 46 为 3 的左子树, 57 为 3 的右子树, 前序序列 4、6 应相连, 5、7 应相连, 不符题意。
解法 2: 前序遍历时需要借助栈。二叉树的前序序列和中序序列的关系相当于以前序序列作为入栈次序, 以中序序列作为出栈次序。题中以 1234567 入栈;
对于 A, 第一个出栈的是 3, 所以 1 不可能在 2 之前出栈,错误。对于 不可能在 3 之前出栈,错误。对于 第三个出栈, 此时栈顶元素是 5, 不是 3, 错误。B 正确。
解法 3: 因前序序列和中序序列可以确定一棵二叉树, 所以可试着用题目中的序列构造出相应的二叉树,即可得知,只有选项 的序列可以构造出二叉树。