关键路径

首先跟着我默念三遍
事件就是点
活动就是边

回到盖房子的例子。从开始到结束有很多条路径，每条路径的总时间就是路径上所有活动时间的总和。在AOE网中，从起点到终点的所有路径中，时间最长的那条路径就是关键路径。

为什么关键路径很重要？

因为关键路径决定了整个工程完成的最短时间。如果关键路径上的任何一个活动延迟了，整个工程的完成时间就会延迟。就像盖房子，如果砌墙（关键路径上的活动）延迟了，那么装屋顶也必须延迟，整个房子就盖晚了。

在上面的例子中：

只有一条路径： A ⇒ B ⇒ C，总时间是 3 + 4 + 2 = 9 天。所以这条路径就是关键路径，整个工程的最短完成时间是9天。

关键活动：

关键路径上的活动叫做关键活动。在上面的例子中，A、B、C都是关键活动。

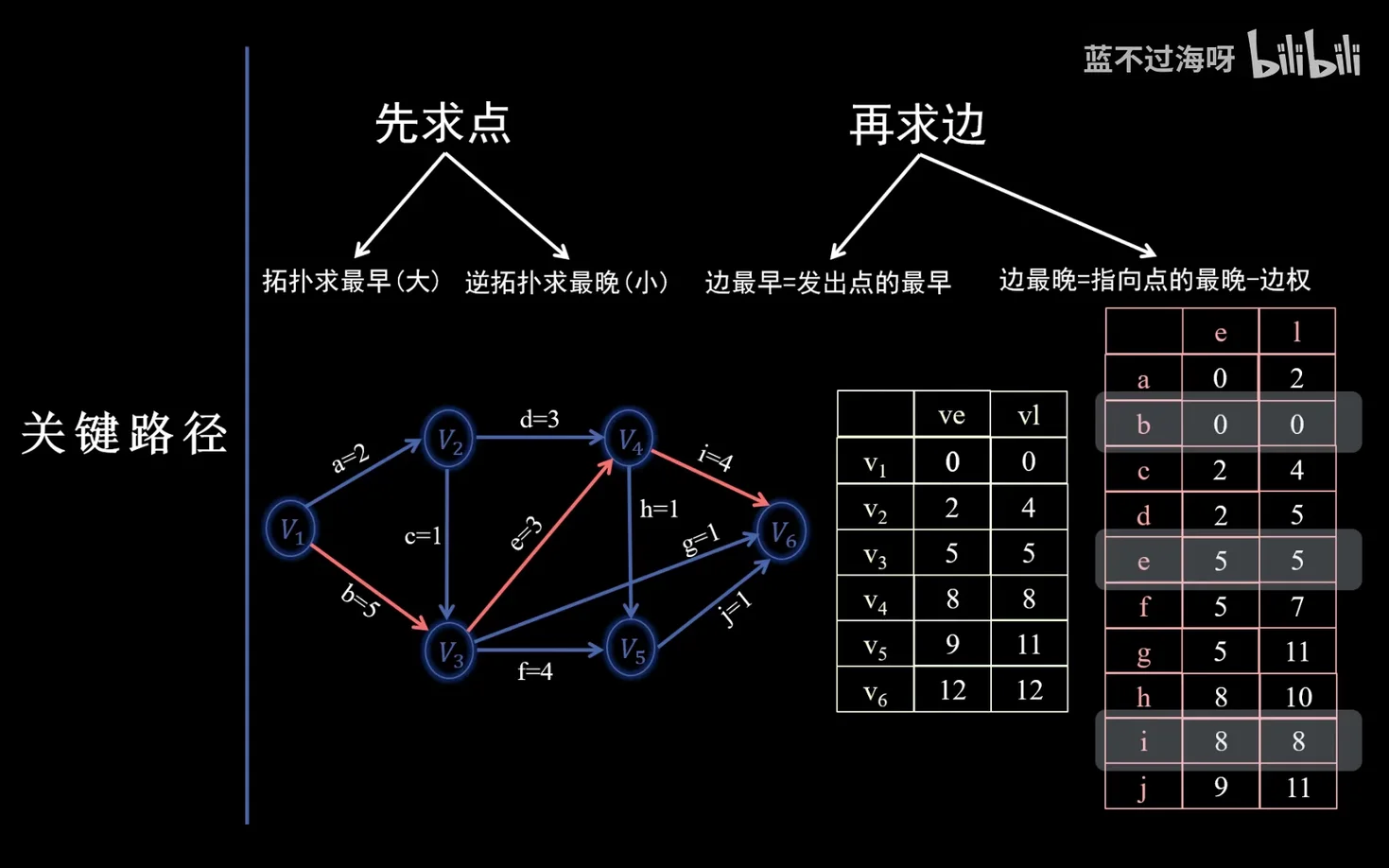
AOE网中的关键路径是从源点到汇点的路径长度最长的那条路径。确定关键活动的核心思想是找到那些最早开始时间和最迟开始时间相同的活动，也就是边。
这些活动被称为关键活动，因为它们任何的延迟都会直接导致整个工程的延迟。它们就像一条链子上的关键环节，缺一不可。

简要概括核心思想：关键活动 = 最早开始时间 == 最迟开始时间

具体步骤和运行逻辑

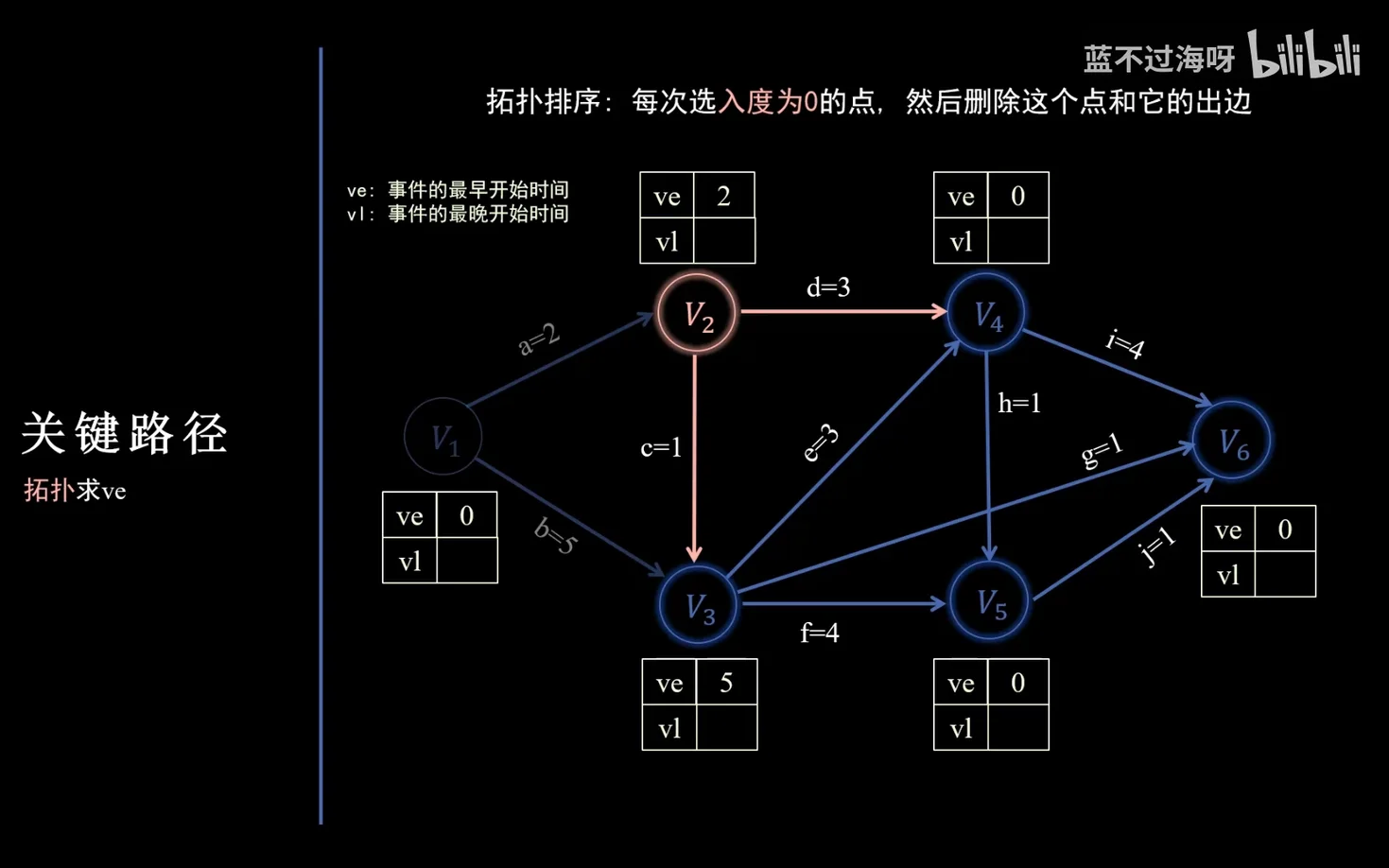
1. 求所有事件（点）的最早发生时间 ve(vk)：感觉像是松弛操作+拓扑排序的混合
   
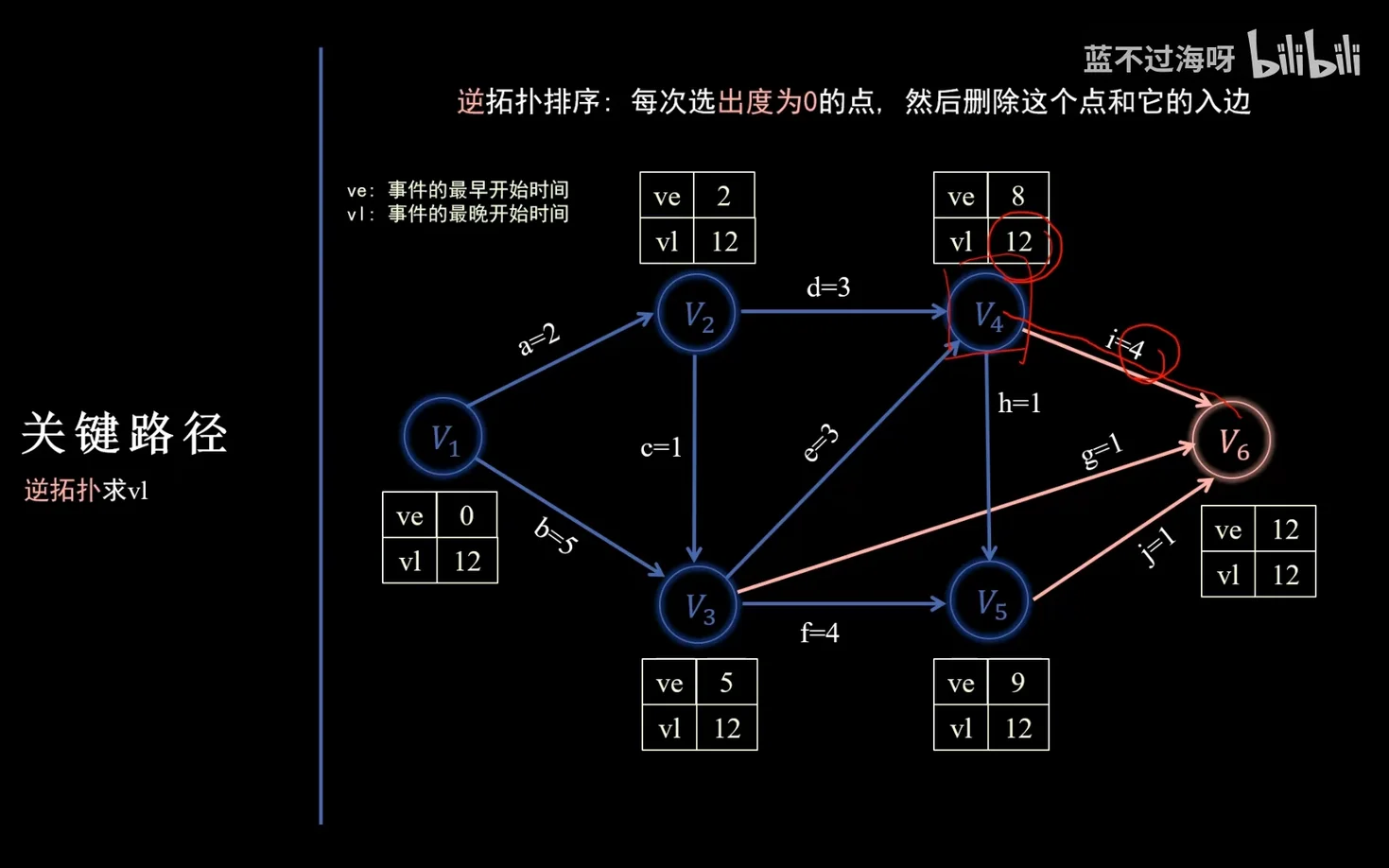
2. 求所有事件的最迟发生时间 vl(vk)：逆拓扑排序+松弛操作（做差取更小的）
   
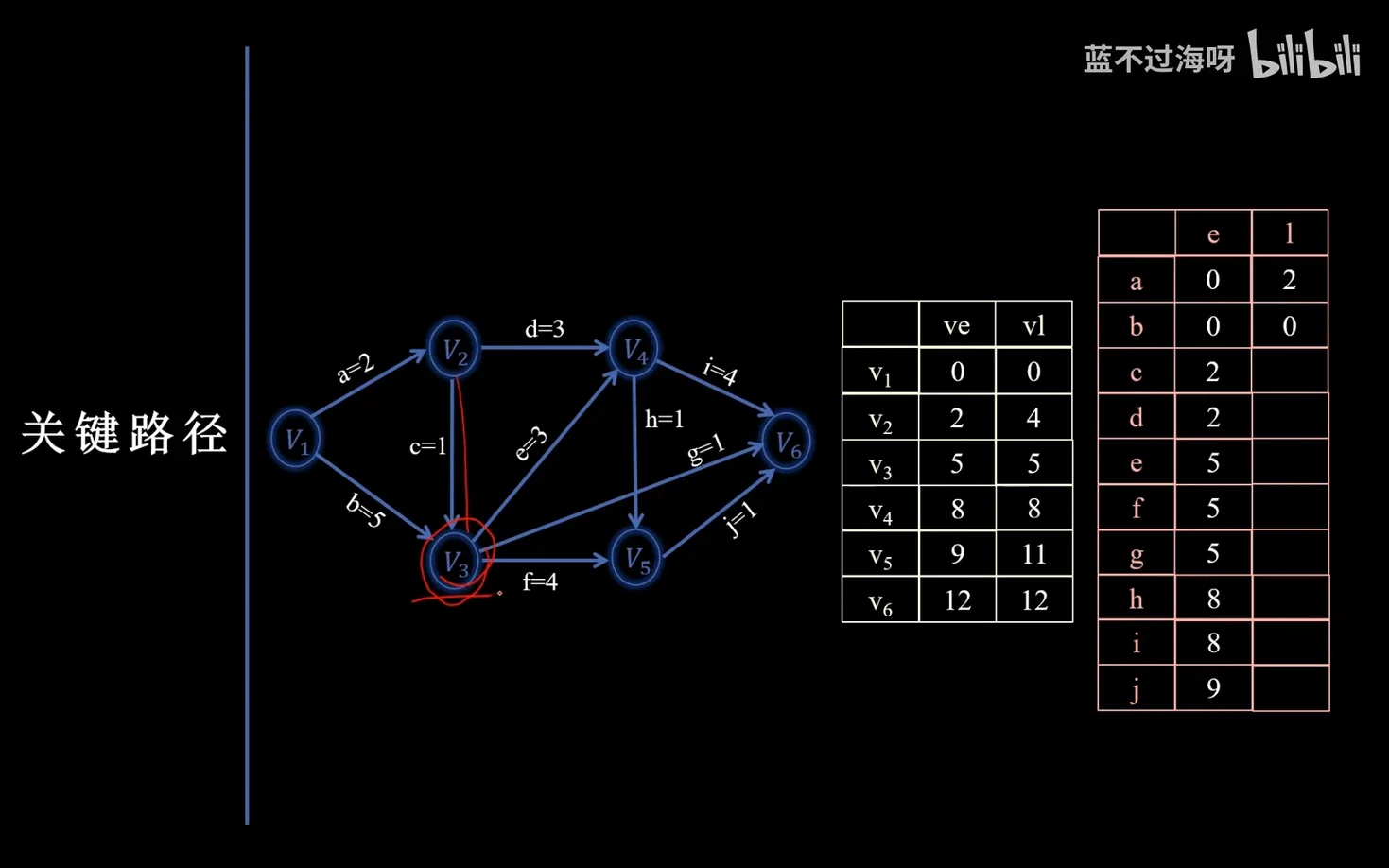
3. 求所有活动的最早发生时间 e(ai)：找这个边是哪个点的出边
   
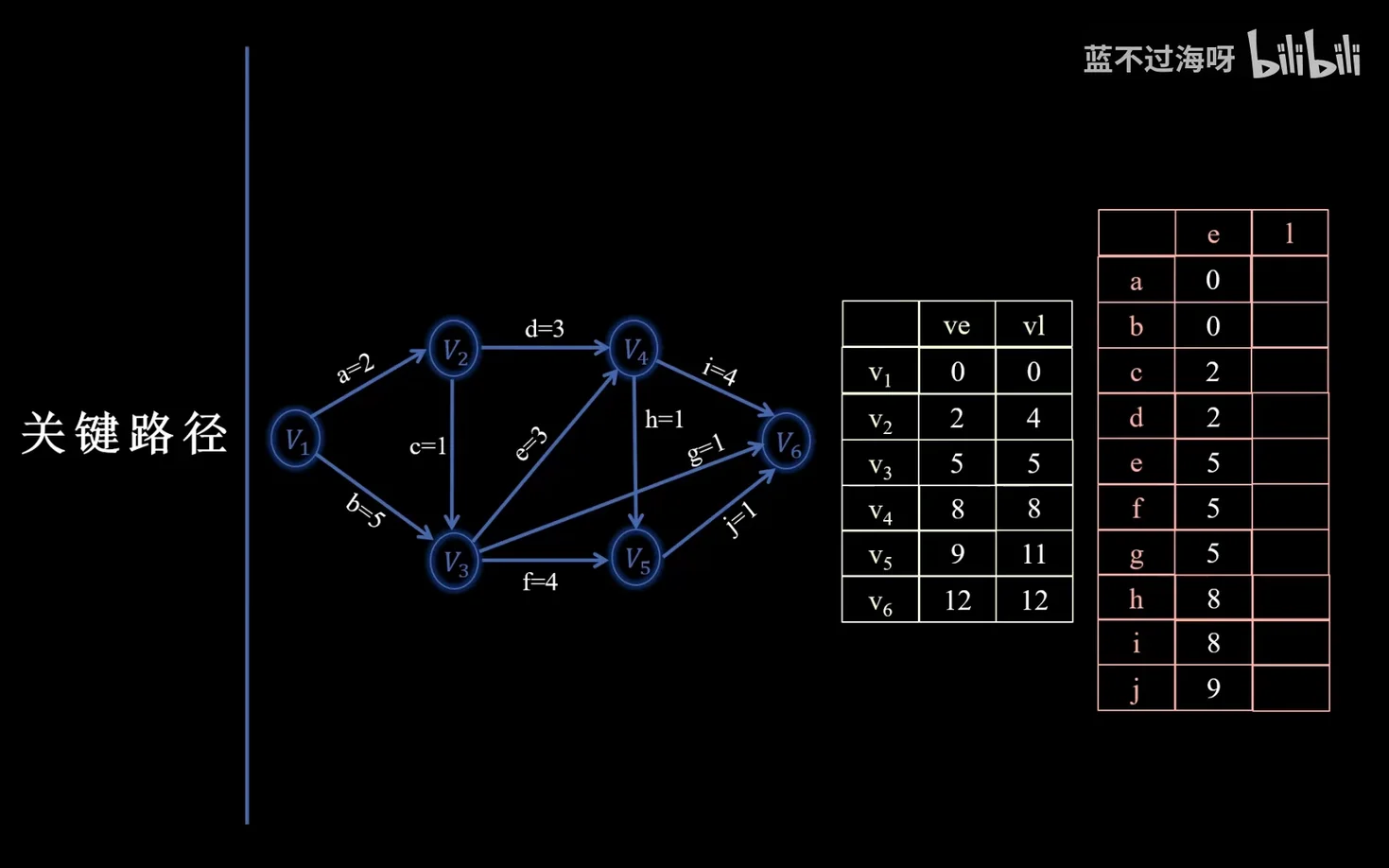
   • 每个活动 ai 的最早发生时间等于该活动起点的最早发生时间，即 。
4. 求所有活动的最迟发生时间 l(ai)：找这个边是哪个点的入边，然后用这个点的最晚时间-边权值
   
   • 每个活动 ai 的最迟发生时间等于该活动终点的最迟发生时间减去该活动的持续时间（边权值），即 。
5. 求所有活动的时间余量 d(ai)：
   • 每个活动 ai 的时间余量等于该活动的最迟发生时间减去最早发生时间，即 。
   • 理解： 时间余量表示一个活动可以延迟多久而不影响整个工程的进度。
6. 确定关键活动和关键路径：
   • 时间余量为 0 的活动就是关键活动，即 。
   • 将所有关键活动连接起来就构成了关键路径。