题21

题21

题目

已知函数 在 上连续,在 内是函数 的一个原函数,且 .
( I ) 求 在区间 上的平均值;
( II ) 证明 在区间 内存在唯一零点.

分析

这道题的第二问我们要积累一下什么时候可以考虑用积分的区间再现公式？另外就是在何种积分套积分，尤其是，定积分套变限积分来做处理的题目，非常常见，真题考察了很多次
这个题目也是第一次看见直接考察，函数的均值这个点

解

分析 本题综合考查了原函数、函数在区间上的平均值以及积分中值定理等知识.

积分中值定理 若函数 在 上连续,则在 上至少存在一点 ,使得

积分中值定理的几何意义 若 ,则左端积分所表示的曲边梯形的面积等于以 为底,以 为高的矩形面积.

函数 在区间 上的平均值为 . 由积分中值定理可知, 即 在 上的平均值.

要求函数在 上的平均值,可以先根据定义写出平均值的表达式,然后再考虑如何计算.

第 ( II ) 问是利用导数来分析函数的零点、单调性等性质的综合问题. 由已知条件可知 的导数 ,于是可以利用它来分析 的单调性.

解 (I) 由于 是 的一个原函数,故不妨设 . 由 可知, . 于是,

根据 在区间 上的平均值的定义,可知

(法一) 我们可以使用分部积分法来处理 (1) 式中的 .

由上可知, . 记 ,则

因此, .

(法二) (1) 式右端分式中的分子为一个二次积分. 由于被积函数是仅关于 的函数,故我们不妨交换积分次序,先关于 积分,再关于 积分.

该二次积分对应的二重积分的积分区域为

将区域 写成 型区域,得

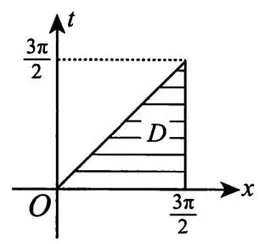
因此,

(II) . 由于在 内, ,而在 内, ; 在 内, ,故在 内, 单调减少,在 内, 单调增加.

由于 ,而 在 内单调减少,故 在 内无零点.

若 ,则由连续函数的零点定理以及单调性可知, 在 内存在唯一零点.

下面我们用两种方法来证明 .

(法一) 由第( I ) 问知,

另一方面, 在 内单调减少,在 内单调增加. 若 ,则 在 内恒小于零, . 矛盾.

因此, .

(法二) 通过换元对 进行估计.

对第三个积分换元,令 ,得 .

因此,

注 (I) 问中的法一使用了分部积分法, 比较巧妙. 法二用到了交换二次积分的次序. 这个想法也是比较自然的,符合我们简化计算的思想. 一般地,对一个关于 的二次积分来说,若被积函数是仅关于 的函数,则先对 积分,再对 积分能使计算简化.