题16

题16

题目

设函数 ，求 ,并求 的最小值.

分析

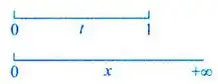
第一步：确定积分变量，这里对t积分，那么t是限制在(0~1)这个范围里面的

对函数进行积分的时候，如果不确定参数是否落入积分变量的积分区域中，或者说讨论绝对值的正负的时候，要分成两部分看，尤其注意，参数在积分区间里和被积分变量的积分，应该变成变限积分，这种题我总是算得不是很熟练：例9.27
也就是下面这个图

解

解 对 的取值范围进行讨论. 由 知,

• 当 时, .
• 当 时,有两种情况.

于是,当 时,

当 时,

当 时,

因此, 从 的表达式可以看出,

在 处连续.

由 的表达式可知,当 时, ; 当 时, . 当 时,根据导数的定义分别计算 在 处的左侧导数和右侧导数.

由此可见, .

因此,

从 的表达式可以看出, 连续,从而 是一条光滑曲线.

当 时, ,故 在 内单调增加.

当 时, . 求 的零点得, 或 (舍去). 因此,当 时, ; 当 时, .

由于 连续,故可知 的最小值在 处取得. .

注 ① 在说明 是 在 上的最小值点时,我们强调了 的连续性. 若 不连续,则 可能不是最小值点. 考虑下面的例子. 令 少,但 不是 在 上的最小值.

② 在求 和 时,我们可以使用 2009 年第 (21) 题第 ( II ) 问中的结论的推广:

若函数 在 处连续,在 内可导,且 ,则 存在,且 .

由于 在 处连续,且 和 在 处均连续,故