反常积分所谓的反常，反的是什么常？
反常积分违反了普通定积分能积出来东西的充要条件，是反的这个常
定积分存在的充要条件：函数在
在 连续 / 有限个第一类间断点，则可积 (可积) - 可积必有界，有界不一定可积
以黎曼积分的定义来看 单调函数可积 (反例：单调函数不一定在闭区间)
根据反的充要条件的不同反常积分分为了两类
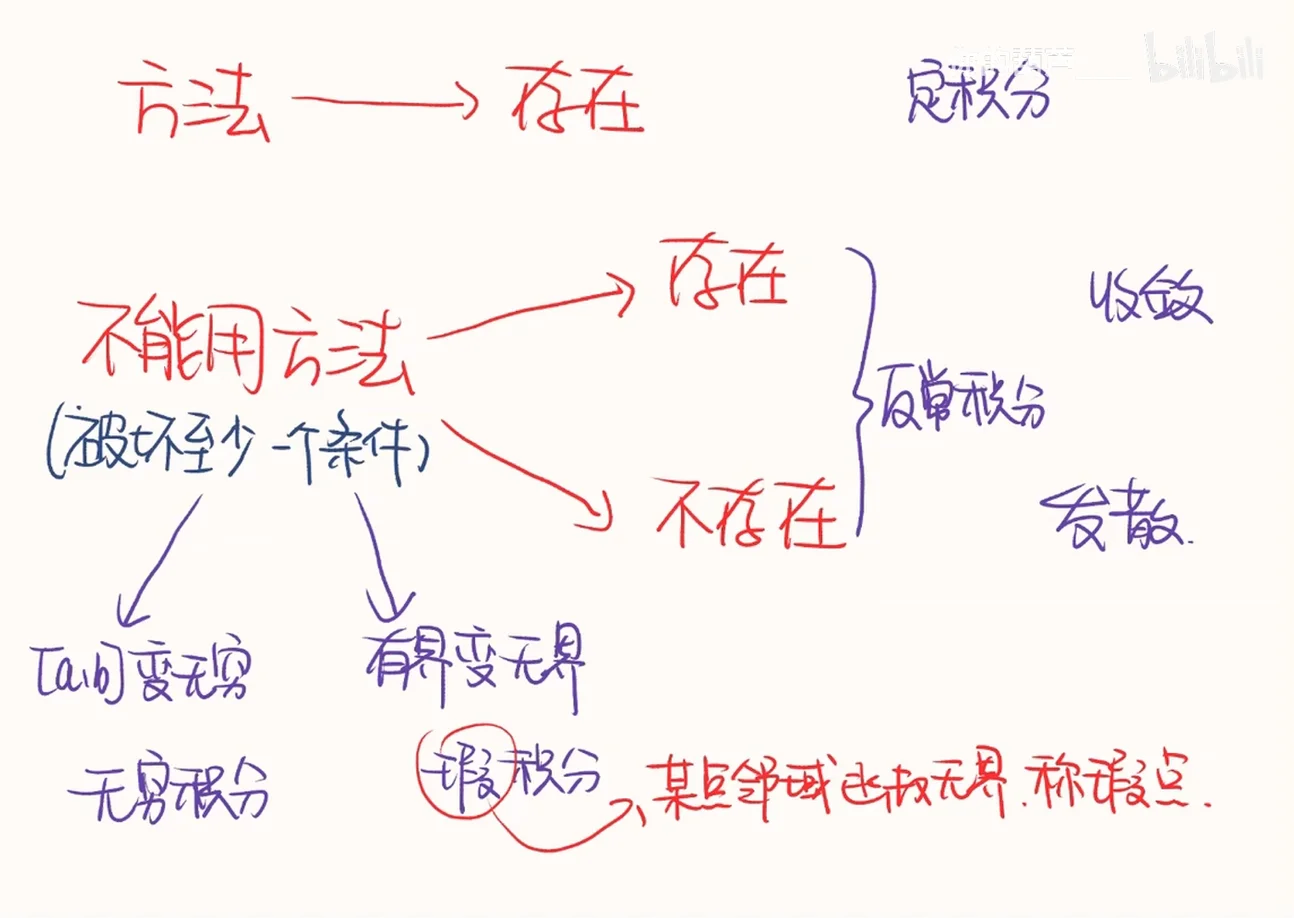
- 无穷区间上的反常积分违背的是
这个闭区间的有界性 - 区间变无穷
- 瑕积分违背的是
这个函数的有界性，在瑕点处无界 - 有界变无界
而无论是哪一类，根据反常积分能不能积出来，分为了
- 有界变无界
- 收敛
- 发散
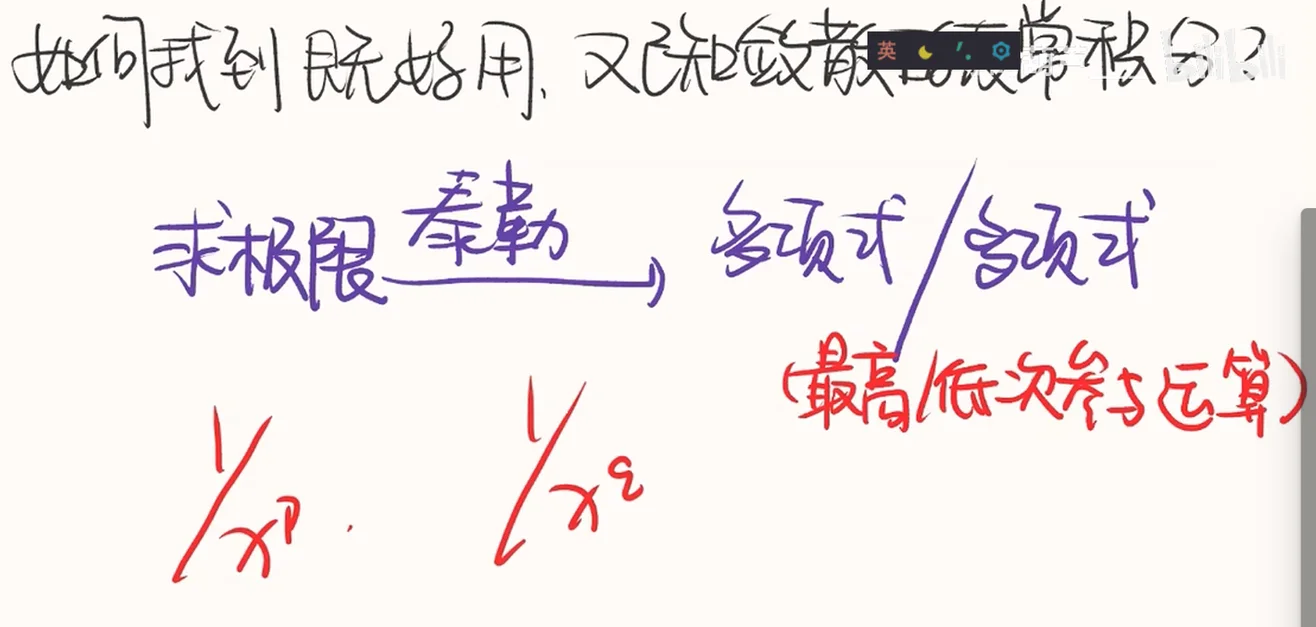
那么如何判断反常积分是收敛还是发散呢？
首先第一步，我们要明确反常积分有哪些反常点
然后，我们需要把反常积分的函数和一个我们熟悉的已知敛散性的函数进行比较
下面这里的这个点是，反常的点
接下来就涉及到，如何去找到这个分母上的已知敛散性的函数？
因为我们在比较这个比值的极限时，看它是否收敛，这是一个取某点上的趋势，满足各种无穷小和无穷大，只用看最高次，于是我们抽象出只有最高次的p积分或者广义p积分；对于瑕积分，也就是p积分-瑕积分
如何记忆无穷区间上的p积分呢，本质上这是一个求极限的问题，以例8.9为例
首先还是找到这个要分类的点，对于
我们在1处讨论分开，因为
让x趋近于无穷大，看
怎么算这种无穷区间上的反常积分？
我们来一步一步地解释为什么当
时，反常积分 会发散。 1. 理解反常积分:
首先，我们要明确这个积分是反常积分，因为它积分的上限是无穷大 (
)，不符合常规定积分的定义 (积分区间有限)。 2. 计算反常积分:
对于这种反常积分, 我们要用极限来处理:
- 把无穷大(
) 替换成一个变量 , - 然后计算这个变量趋近于无穷大时的积分值。
具体来说：
3. 分情况讨论:
接下来，我们需要对
的值进行分类讨论：
当
时： 积分变成:
因为
当 趋近于无穷大时，其值也趋近于无穷大，所以这个积分 发散。 当
时： 积分变成:
现在，我们需要根据
与 1 的大小关系来判断积分的敛散性:
如果
, 那么 : 此时，当 趋近于无穷大时， 也趋近于无穷大， 导致整个式子趋近于无穷大，所以积分 发散。 如果
, 那么 : 此时，当 趋近于无穷大时， 趋近于 0， 整个式子趋近于 ，是一个有限值，所以积分 收敛。 4. 结论:
综上所述，当
时, 反常积分 发散。
对于
给定区间区间内收敛，无穷区间，区间内发散
现在明确了比较的标尺，我们就要来处理需要判别的函数
判别步骤
Step 1: 找反常点，分段
，瑕点各在一段。 - 不要随便用偶倍奇零。
- 理解瑕点的哪部分参与积分。
为瑕点： 右侧，积分下限 左侧，积分上限 双侧
- 瑕积分的参数范围可能存在定积分情况
Step 2: 选择比较函数
: :
瑕点: : 为积分下限，是瑕点，a的右侧到b参与积分 - 把标准情况
- 平移到
处
: - a是积分上限，同时a是瑕点，a的左侧的一部分参与积分
- 区间长度无所谓，主要是瑕点在上限还是下限
- 保证q里面是正数
: 中间分开后使用上述两种
Step 3: 找“三类”
比值为
则一定可判别成功。
故希望找到这样的 p,q
但有的情况找不到…
以下面两道题为例
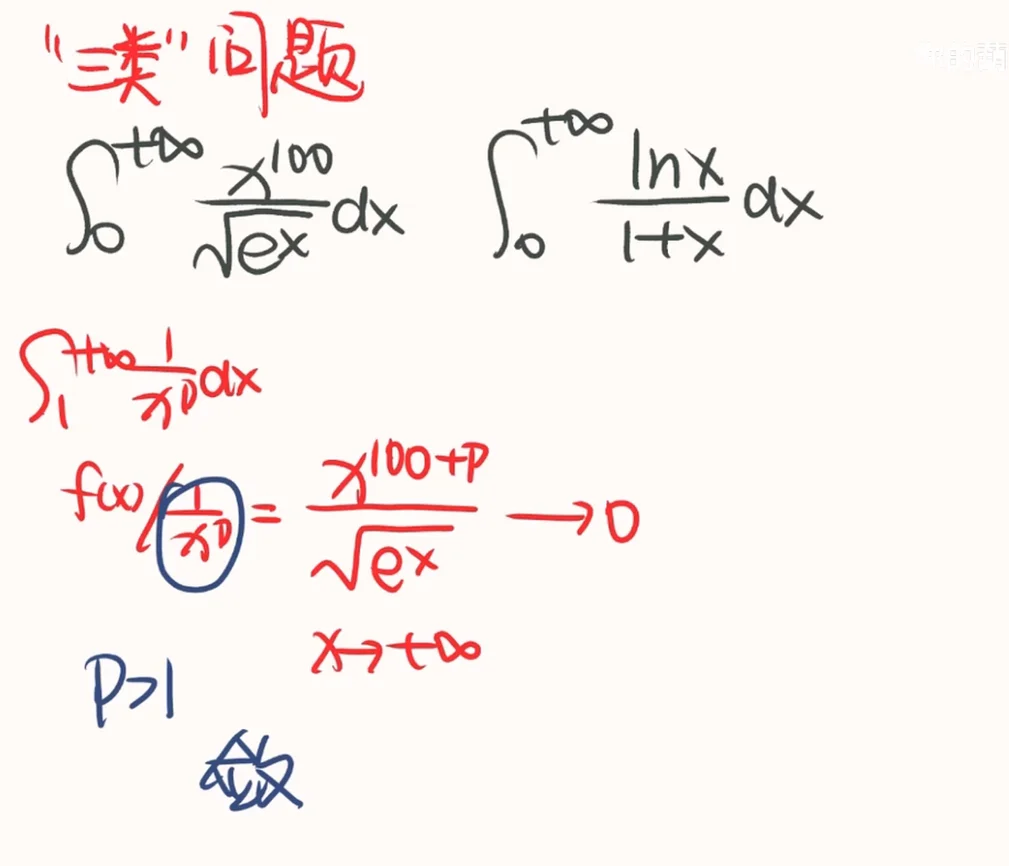
Step4: 建立极限过程并求解 (不含三类)
最后：综合判断
- 如果分段积分中有一段发散，则原反常积分发散。
- 如果分段积分中所有段都收敛，则原反常积分收敛。
(如果能够求出原函数，例如