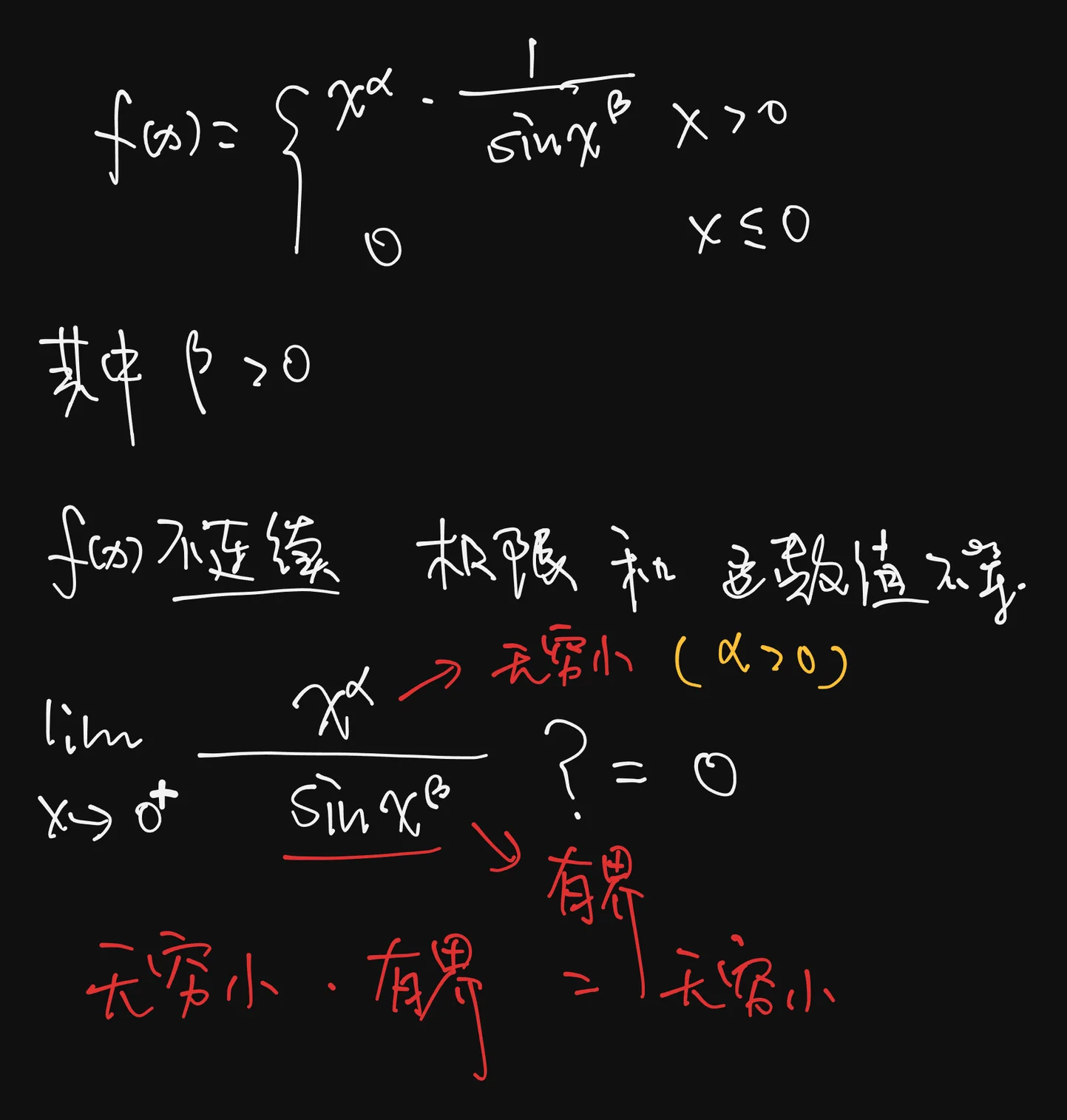例3.9
题目
Q:P98 设 其中 是常数,且 .
(1) 在什么情况下, 不是连续函数?
(2) 在什么情况下, 连续但不可微?
(3) 在什么情况下, 可微,但 在 上无界?
(4) 在什么情况下, 可微,且 在 上有界,但 不连续?
(5) 在什么情况下, 连续?
分析
A:例3.9-2024-09-29-14-15-32.excalidraw
考察可微和可导的定义
无穷小乘以有界,结果是无穷小
解
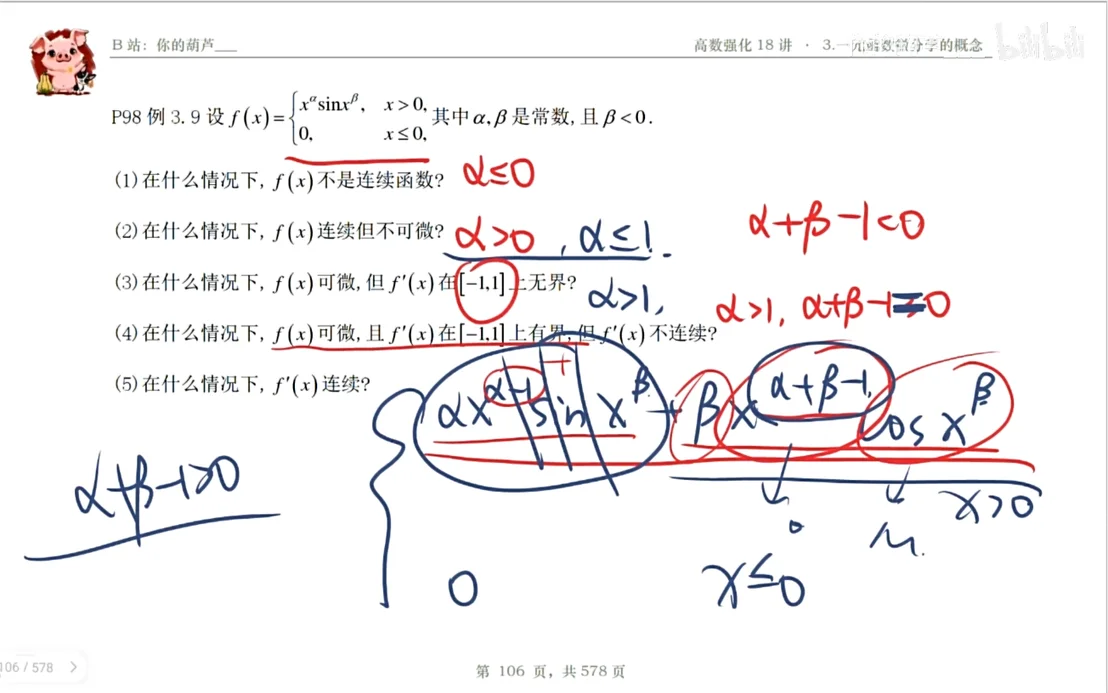
【解】 的定义域为 ,显然,只有分段点 对题中每一个问题的结论是否成立有影响,故只需针对 进行讨论.
(1) 欲使 在点 处不连续,只需极限 不存在,即只需
亦即 . 故当且仅当 时, 在 处不连续.
(2) 由 (1) 知,当 时, 是处处连续的函数. 欲使 在 处不可微,只需极限
不存在,即只需 . 因此,当 时, 在 处连续但不可微.
(3) 由 (2) 知,当 时, 在 处可微,且
由 的表达式知,要使 在 上无界,只需 .
因此,当 且 ,即 时, 可微,但 在 上无界.
(4) 由 (3) 知,当 时, 在 上有界. 要使 在 处不连续,只需 ,即只需 .
因此,当 时, 可微, 在 上有界,但 不连续.
(5) 由 (4) 知,当 时, 连续.
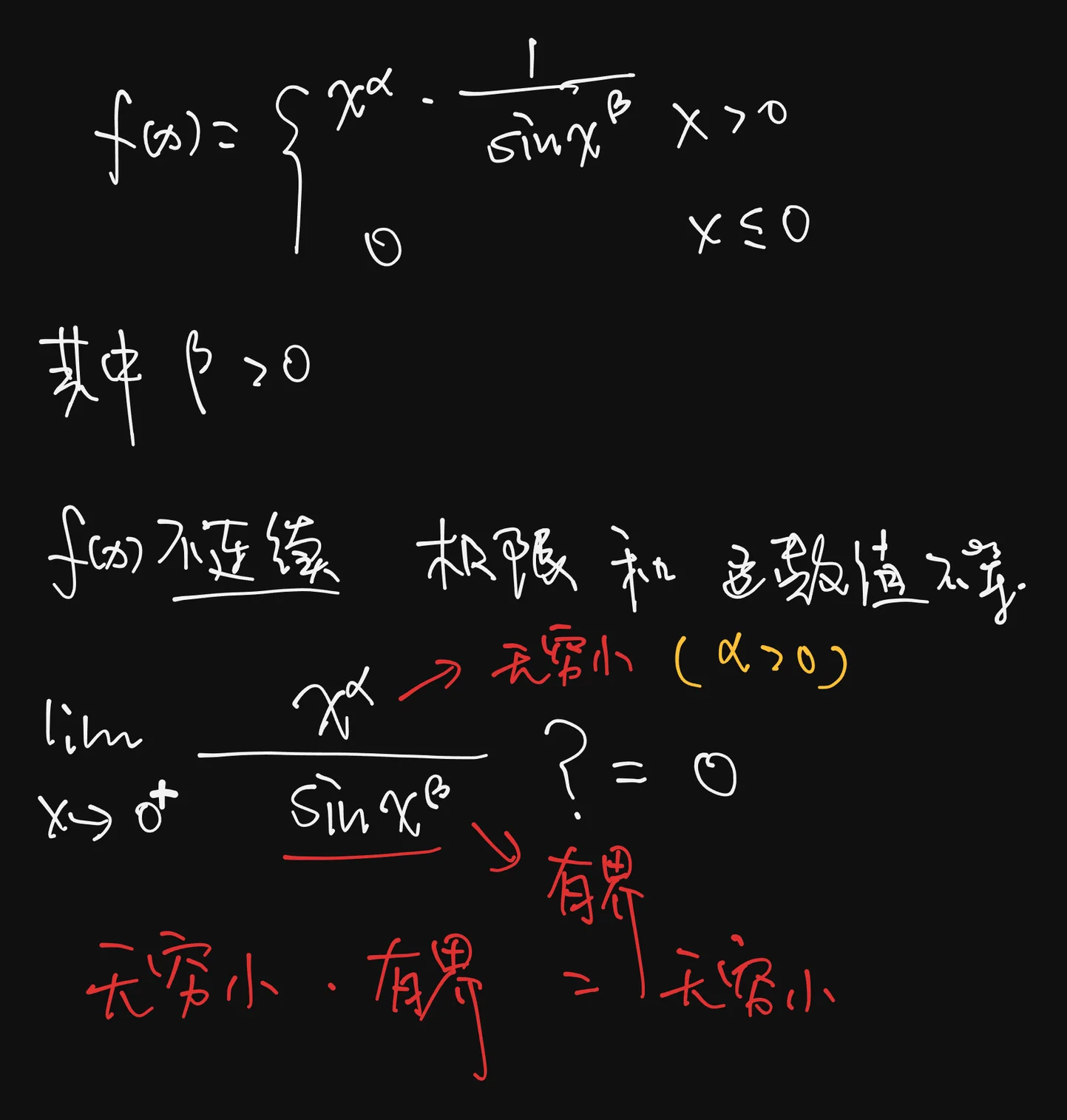
Q: ,或 ,则
A:【注】