题22
题目
[!question]+
设
( I ) 计算行列式
(II) 当实数
分析
[!NOTE]+
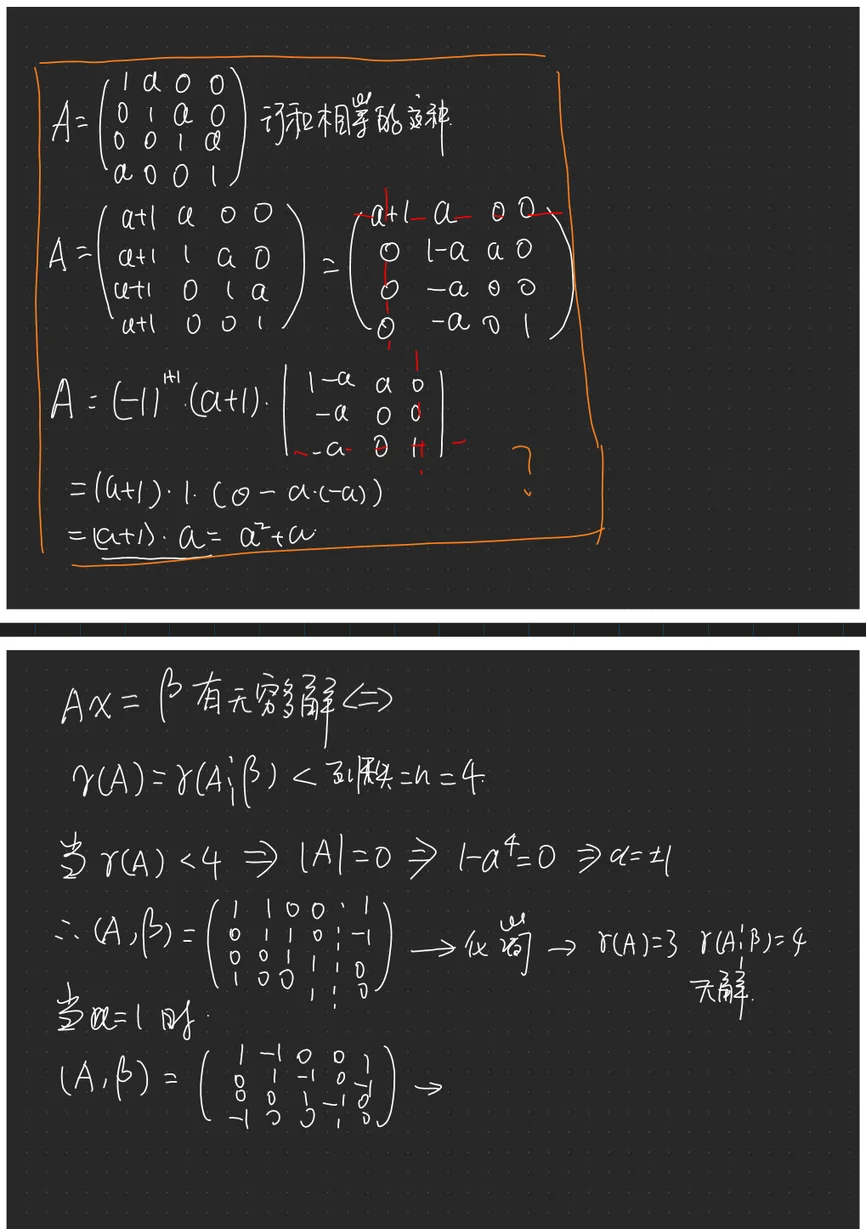
解
[!done]-
对本题而言,
解 (I) 按第一行展开
(II) (法一)
由
当
(
由上可知,
当
由上可知,
齐次方程
综上所述,当
(法二) 对含有参数
由于
Jun 19, 20256 min read
[!question]+
设
( I ) 计算行列式
(II) 当实数
[!NOTE]+
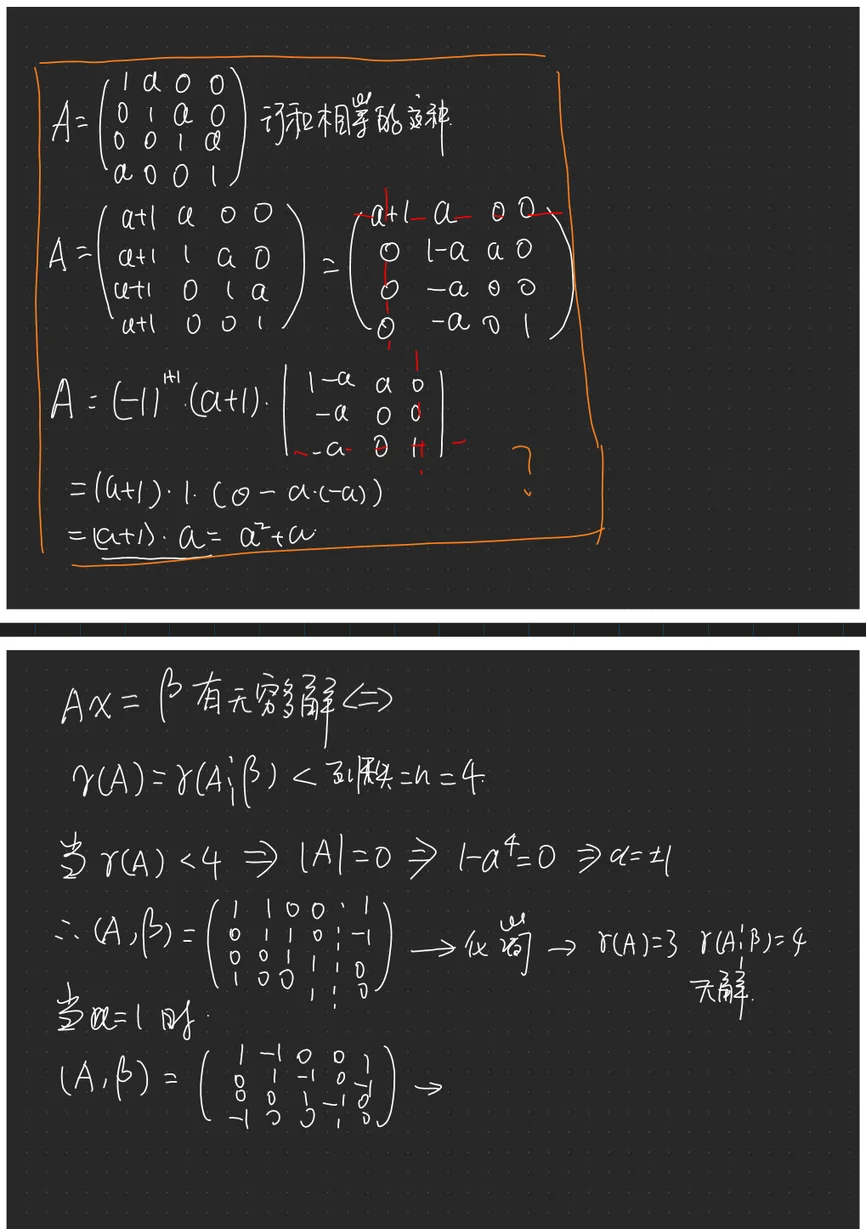
[!done]-
对本题而言,
解 (I) 按第一行展开
(II) (法一)
由
当
(
由上可知,
当
由上可知,
齐次方程
综上所述,当
(法二) 对含有参数
由于