408史上最难算法题：两个升序数组的中位数

真题

2011 年全国硕士研究生招生考试计算机科学与技术学科联考计算机学科专业基础综合试题第 42 题：

一个长度为 的升序序列 ，处在第 个位置的数称为 的中位数。例如，若序列 ，则 的中位数是 。两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若序列 ，则 和 的中位数是 。现有两个等长的升序序列 和 ，试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列 和 的中位数。要求：

1. 给出算法的基本设计思想。
2. 根据设计思想，采用 C 或 C++ 或 Java 语言描述，关键之处给出注释。
3. 说明你所设计算法的时间复杂度和空间复杂度。

本题 15 分，第一问 5 分，第二问 8 分，第三问 2 分。

题源

我开始定位这道题的出处为力扣 (LeetCode)4. 寻找两个正序数组的中位数 (4. Median of Two Sorted Arrays)。

实际情况是这道题的出处是《算法导论》第三版 9.3-8，现《算法导论》第四版 9.3-10，原题如下：

Let and be two arrays, each containing n numbers already in sorted order. Give an -time algorithm to find the median of all elements in arrays and . Assume that all numbers are distinct.

本人从 2022 年 8 月 8 日开始学习《算法导论》第九章，直至 2022 年 8 月 17 日，本题最优解才算完全整理出来，实在不容易，本人之前提供题解的部分有误，已经进行订正，对之前阅读本题的同学致歉。感兴趣的同学也可以阅读原题：算法导论（第四版）第九章：中位数和顺序统计量　第三节：最坏情况为线性时间的选择算法

真题在原题的基础上进行了改编，原题假设所有数均不同，去掉这一条件难度略有提升，但是不影响解题思路。

题解

解答：

设两个数组的长度均为 ，总计 个数，注意 C 或 C++ 或 Java 语言数组下标从 0 开始。

本题解法有很多，我下面一一枚举（如果觉得太长可以先看总结）：

方法一：合并数组

本方法为朴素解法，将两个数组合并后取第 个数。开辟辅助空间 记录合并后的数组，最后返回 。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int findMedianSortedArrays(int* A, int* B, int n) {
    int C[n << 1];
    int i = 0, j = 0, p = 0;
    while (i < n && j < n) {
        if (A[i] <= B[j]) {
            C[p++] = A[i++];
        } else {
            C[p++] = B[j++];
        }
    }
    while (i < n) {
        C[p++] = A[i++];
    }
    while (j < n) {
        C[p++] = B[j++];
    }
    return C[n - 1];
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = A.size();
    vector<int> C(n << 1);
    int i = 0, j = 0, p = 0;
    while (i < n && j < n) {
        if (A[i] <= B[j]) {
            C[p++] = A[i++];
        } else {
            C[p++] = B[j++];
        }
    }
    while (i < n) {
        C[p++] = A[i++];
    }
    while (j < n) {
        C[p++] = B[j++];
    }
    return C[n - 1];
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：7 分，主体思路正确，但时间复杂度和空间复杂度都有较大优化空间。

这里代码可以进一步优化，开辟辅助变量 记录合并后的数组的前 个元素的最后一个元素，最后返回 。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int findMedianSortedArrays(int* A, int* B, int n) {
    int last;
    int i = 0, j = 0, p = 0;
    while (i < n && j < n) {
        if (A[i] <= B[j]) {
            last = A[i++];
        } else {
            last = B[j++];
        }
        if (++p == n) {
            break;
        }
    }
    return last;
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = A.size();
    int last;
    int i = 0, j = 0, p = 0;
    while (i < n && j < n) {
        if (A[i] <= B[j]) {
            last = A[i++];
        } else {
            last = B[j++];
        }
        if (++p == n) {
            break;
        }
    }
    return last;
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：8 分，主体思路正确，但时间复杂度有较大优化空间。

方法二：基于值域的二分查找

基于值域的二分查找是找有序数组第 K 小的元素的固定模板，即在最小值和最大值之间通过二分查找选择一个阈值，使得数组 和 中不超过该阈值的元素个数恰巧为 个，则该阈值为中位数。

详见本人力扣原创题解多重二分查找 + 多维度二分查找。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int max(int x, int y) {
    return x > y ? x : y;
}
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
// 查找数组中小于等于threshold的元素个数，二分查找横坐标元素下标
int getCount(int *nums, int n, int threshold) {
    int l = 0, r = n - 1;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (nums[mid] <= threshold) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return r + 1;
}
 
int findMedianSortedArrays(int* A, int* B, int n) {
    int l = min(A[0], B[0]), r = max(A[n - 1], B[n - 1]);
    while (l <= r) {
        int mid = (l + r) / 2;
        if (getCount(A, n, mid) + getCount(B, n, mid) < n) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return l;
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
// 查找数组中小于等于threshold的元素个数，二分查找横坐标元素下标
int getCount(vector<int>& nums, int threshold) {
    int l = 0, r = (int)nums.size() - 1;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (nums[mid] <= threshold) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return r + 1;
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    const int n = (int)A.size();
    int l = min(A[0], B[0]), r = max(A.back(), B.back());
    while (l <= r) {
        int mid = (l + r) / 2;
        if (getCount(A, mid) + getCount(B, mid) < n) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return l;
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： ，其中 为数组值域大小。
• 空间复杂度： 。

个人评分：10 分，主体思路正确，但时间复杂度有较大优化空间。

方法三：基于元素值的二分查找

方法二中通过二分查找值域选择一个值，从而时间复杂度在 的基础上多了一个 的因数。其实这个值可以直接在数组中选取，从而优化时间复杂度为 。

可参考《算法导论》的教师手册 Instructor’s Manual for Introduction to Algorithms (Third Edition) 提供的官方题解思路，注意伪代码和高级语言的区别，伪代码数组下标从 1 开始，C/C++ 数组下标从 0 开始。

下面对此伪代码进行改写。C/C++ 中数组下标从 0 开始，用 INT_MAX 代表伪代码中 NOT-FOUND。

我们先假设中位数位于 中第 个顺序统计量 ，则 有 个元素小于或等于 ， 有 个元素大于或等于 。如果两个数组合并后，有 个元素小于或等于 ， 有 个元素大于或等于 ，则 有 个元素小于或等于 ， 有 个元素大于或等于 ，则必然有 成立，同时我们要考虑边界情况，如果 ，我们只需要 成立。

如果上述不等式不成立，假设中位数位于 中为 ， ，则 比中位数大，有 。相反的，假设中位数位于 中为 ， ，则 比中位数小，有 。

这样，我们可以对中位数进行二分查找，如果最后在 中没有找到中位数，则该中位数一定在 中，然后用同样的方法在 中查找中位数。

C 代码如下（含测试用例）：

#include <stdio.h>
#include <limits.h>
 
int findMedian(int *A, int *B, int n, int low, int high) {
    if (low > high) {
        return INT_MAX;
    } else {
        int k = (low + high) / 2;
        if (k == n && A[k - 1] <= B[0]) return A[k - 1];
        else if (k < n && B[n - k - 1] <= A[k - 1] && A[k - 1] <= B[n - k]) return A[k - 1];
        else if (A[k - 1] > B[n - k]) return findMedian(A, B, n, low, k - 1);
        else return findMedian(A, B, n, k + 1, high);
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    int median = findMedian(A, B, n, 0, n - 1);
    if (median == INT_MAX) median = findMedian(B, A, n, 0, n - 1);
    return median;
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedian(vector<int>& A, vector<int>& B, int n, int low, int high) {
    if (low > high) {
        return INT_MAX;
    } else {
        int k = (low + high) / 2;
        if (k == n && A[k - 1] <= B[0]) return A[k - 1];
        else if (k < n && B[n - k - 1] <= A[k - 1] && A[k - 1] <= B[n - k]) return A[k - 1];
        else if (A[k - 1] > B[n - k]) return findMedian(A, B, n, low, k - 1);
        else return findMedian(A, B, n, k + 1, high);
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = (int)A.size();
    int median = findMedian(A, B, n, 0, n - 1);
    if (median == INT_MAX) median = findMedian(B, A, n, 0, n - 1);
    return median;
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

我们比较下方法三和方法四，方法三是划分数组后基于分割线的二分查找，优点是只需要遍历一次，缺点是需要构造边界；方法四是划分数组后基于比较的二分查找，优点是不会越界，缺点是中位数可能不在第一个被查找的数组中，需要去另外一个数组中查找。

个人评分：14 分，主体思路正确，时间复杂度和空间复杂度均为最优，唯一缺点是引入未找到的特殊值 INT_MAX，本题没有给出数据范围。

方法四：基于分割线的二分查找

参考力扣官方题解寻找两个有序数组的中位数方法二划分数组解法。

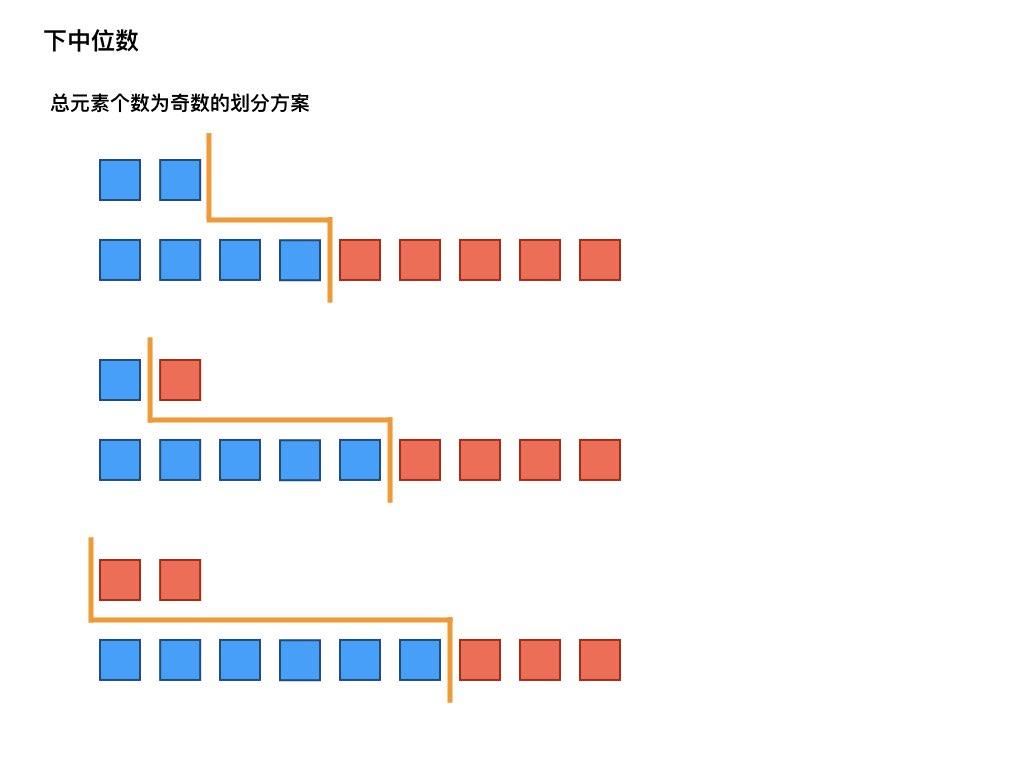
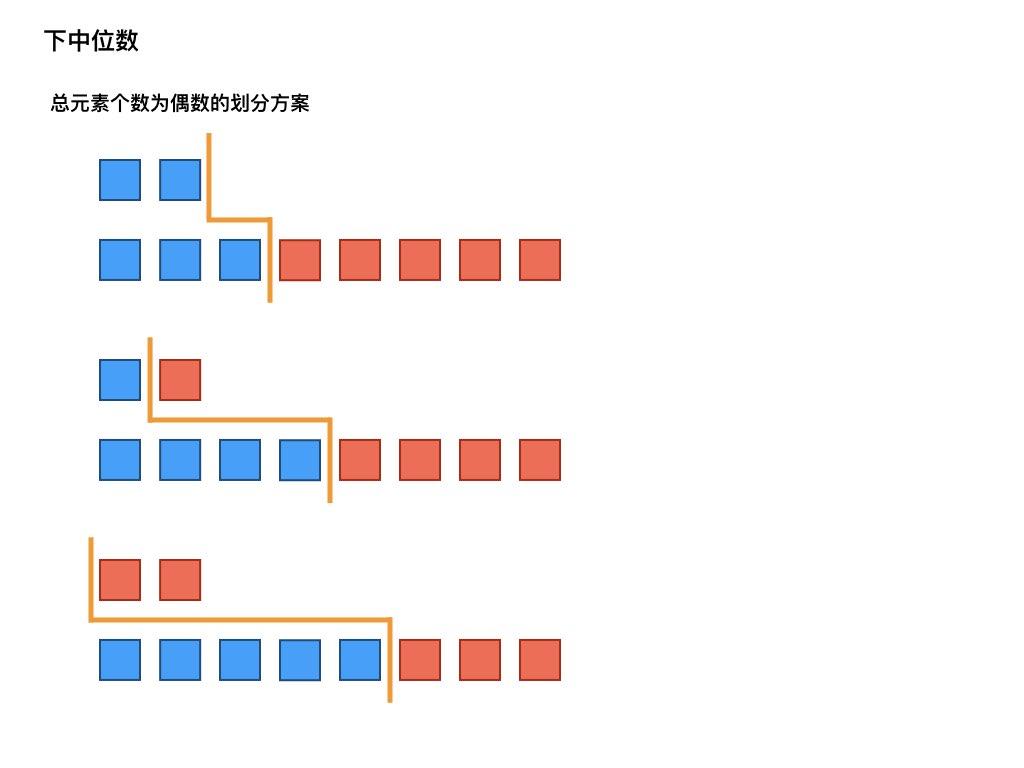
把每个数组各用一条分割线划分为两部分，通过二分查找确定两条分割线位置。

由于这里选择下中位数，我们进行这样划分，如果总元素个数为偶数，两个分割线左边元素总和 = 两个分割线右边元素总和，如果总元素个数为奇数，两个分割线左边元素总和 = 两个分割线右边元素总和 + 1。

二分查找的数组元素有 个，则分割线位置有 个，编号 ，构造二分查找左右指针， 初始时，左指针指向 0，右指针指向 ；

设两个数组分别为 ，数组 分割线左侧元素为 ，数组 分割线由侧元素为 ，数组 分割线左侧元素为 ，数组 分割线由侧元素为 ，左侧没有元素设为虚拟的 ，右侧没有元素设为虚拟的 。

二分查找终止时，有 且 ，取 为最终结果。

C 代码如下（含测试用例）：

#include <stdio.h>
#include <limits.h>
 
int max(int x, int y) {
    return x > y ? x : y;
}
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findMedian(int *A, int *B, int n) {
    int left = 0, right = n;
    // median1：前一部分的最大值，最后存下中位数
    // median2：后一部分的最小值，最后存上中位数
    int median1, median2;
    while (left <= right) {
        // 前一部分包含 A[0 : i - 1] 和 B[0 : j - 1]
        // 后一部分包含 A[i : m - 1] 和 B[j : n - 1]
        int i = (left + right) / 2;
        int j = n - i;
        // a1, a2, b1, b2 分别表示 A[i-1], A[i], B[j-1], B[j]
        int a1 = (i == 0 ? INT_MIN : A[i - 1]);
        int a2 = (i == n ? INT_MAX : A[i]);
        int b1 = (j == 0 ? INT_MIN : B[j - 1]);
        int b2 = (j == n ? INT_MAX : B[j]);
        if (a1 <= b2) {
            median1 = max(a1, b1);
            median2 = min(a2, b2);
            left = i + 1;
        } else {
            right = i - 1;
        }
    }
    return median1;
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findMedian(A, B, n);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedian(vector<int>& A, vector<int>& B) {
    int n = A.size();
    int left = 0, right = n;
    // median1：前一部分的最大值，最后存下中位数
    // median2：后一部分的最小值，最后存上中位数
    int median1, median2;
    while (left <= right) {
        // 前一部分包含 A[0 : i - 1] 和 B[0 : j - 1]
        // 后一部分包含 A[i : m - 1] 和 B[j : n - 1]
        int i = (left + right) / 2;
        int j = n - i;
        // a1, a2, b1, b2 分别表示 A[i-1], A[i], B[j-1], B[j]
        int a1 = (i == 0 ? INT_MIN : A[i - 1]);
        int a2 = (i == n ? INT_MAX : A[i]);
        int b1 = (j == 0 ? INT_MIN : B[j - 1]);
        int b2 = (j == n ? INT_MAX : B[j]);
        if (a1 <= b2) {
            median1 = max(a1, b1);
            median2 = min(a2, b2);
            left = i + 1;
        } else {
            right = i - 1;
        }
    }
    return median1;
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    return findMedian(A, B);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：14 分，主体思路正确，时间复杂度和空间复杂度均为最优，唯一缺点是引入边界值 INT_MIN 和 INT_MAX，本题没有给出数据范围。

方法五：二分查找变体

参考力扣官方题解寻找两个有序数组的中位数方法一二分查找解法。

二分查找本质是保留一部分，舍弃一部分，对其中一个数组应用该思想。

找出第 小的数。

画出有向图，→指向表示有向边，有向边起点元素小于或等于有向边终点元素。

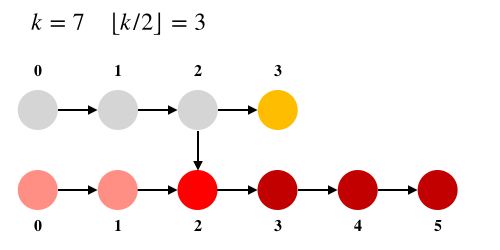
如上图，灰色结点淘汰。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findKthElement(int *a, int *b, int m, int n, int k) {
    int i = 0, j = 0;
    while (1) {
        // 边界情况
        if (i == m) {
            return b[j + k - 1];
        }
        if (j == n) {
            return a[i + k - 1];
        }
        if (k == 1) {
            return min(a[i], b[j]);
        }
 
        // 正常情况
        int ni = min(i + k / 2 - 1, m - 1);
        int nj = min(j + k / 2 - 1, n - 1);
        int x = a[ni];  // pivot of A
        int y = b[nj]; // pivot of B
        if (x <= y) {
            k -= ni - i + 1;
            i = ni + 1;
        } else {
            k -= nj - j + 1;
            j = nj + 1;
        }
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findKthElement(A, B, n, n, n);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findKthElement(vector<int>& a, vector<int>& b, int k) {
    int m = a.size();
    int n = b.size();
    int i = 0, j = 0;
    while (1) {
        // 边界情况
        if (i == m) {
            return b[j + k - 1];
        }
        if (j == n) {
            return a[i + k - 1];
        }
        if (k == 1) {
            return min(a[i], b[j]);
        }
 
        // 正常情况
        int ni = min(i + k / 2 - 1, m - 1);
        int nj = min(j + k / 2 - 1, n - 1);
        int x = a[ni];  // pivot of A
        int y = b[nj]; // pivot of B
        if (x <= y) {
            k -= ni - i + 1;
            i = ni + 1;
        } else {
            k -= nj - j + 1;
            j = nj + 1;
        }
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    return findKthElement(A, B, A.size());
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：13 分，主体思路正确，时间复杂度和空间复杂度均为最优，但没有利用两个数组等长和中位数这一条件，可以继续优化。

修改为递归版代码如下：

递归版本一，保存下标，为原地算法。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findKthElement(int *a, int *b, int m, int n, int pa, int ra, int pb, int rb, int k) {
    if (pa > ra) {
        return b[pb + k - 1];
    }
    if (pb > rb) {
        return a[pa + k - 1];
    }
    if (k == 1) {
        return min(a[pa], b[pb]);
    }
 
    int i = min(ra - pa + 1, k / 2);
    int j = min(rb - pb + 1, k / 2);
    if (a[pa + i - 1] > b[pb + j - 1]) {
        // Discard the first j numbers from B, which can never be the kth number
        return findKthElement(a, b, m, n, pa, ra, pb + j, rb, k - j);
    } else {
        // Discard the first i numbers from A, which can never be the kth number
        return findKthElement(a, b, m, n, pa + i, ra, pb, rb, k - i);
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findKthElement(A, B, n, n, 0, n - 1, 0, n - 1, n);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findKthElement(vector<int>& A, vector<int>& B, int pa, int ra, int pb, int rb, int k) {
    if (pa > ra) {
        return B[pb + k - 1];
    }
    if (pb > rb) {
        return A[pa + k - 1];
    }
    if (k == 1) {
        return min(A[pa], B[pb]);
    }
    
    int i = min(ra - pa + 1, k / 2);
    int j = min(rb - pb + 1, k / 2);
    if (A[pa + i - 1] > B[pb + j - 1]) {
        // Discard the first j numbers from B, which can never be the kth number
        return findKthElement(A, B, pa, ra, pb + j, rb, k - j);
    } else {
        // Discard the first i numbers from A, which can never be the kth number
        return findKthElement(A, B, pa + i, ra, pb, rb, k - i);
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = A.size();
    return findKthElement(A, B, 0, n - 1, 0, n - 1, n);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：13 分，主体思路正确，时间复杂度和空间复杂度均为最优，但没有利用两个数组等长和中位数这一条件，可以继续优化。

递归版本二，这里不保存下标，直接进行数组复制，参数更少，写法更加简单一点。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findKthElement(int *a, int *b, int m, int n, int k) {
    if (m == 0) {
        return b[k - 1];
    }
    if (n == 0) {
        return a[k - 1];
    }
    if (k == 1) {
        return min(a[0], b[0]);
    }
    int i = min(m, k / 2);
    int j = min(n, k / 2);
    if (a[i - 1] > b[j - 1]) {
        // Discard the first j numbers from B, which can never be the kth number
        int nb[n - j];
        for (int t = 0; t < n - j; t++) {
            nb[t] = b[t + j];
        }
        return findKthElement(a, nb, m, n - j, k - j);
    } else {
        // Discard the first i numbers from A, which can never be the kth number
        int na[m - i];
        for (int t = 0; t < m - i; t++) {
            na[t] = a[t + i];
        }
        return findKthElement(na, b, m - i, n, k - i);
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findKthElement(A, B, n, n, n);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findKthElement(vector<int> A, vector<int> B, int k) {
    if (A.empty()) {
        return B[k - 1];
    }
    if (B.empty()) {
        return A[k - 1];
    }
    if (k == 1) {
        return min(A.front(), B.front());
    }
    
    int i = min((int) A.size(), k / 2);
    int j = min((int) B.size(), k / 2);
    if (A[i - 1] > B[j - 1]) {
        // Discard the first j numbers from B, which can never be the kth number
        return findKthElement(A, vector<int>(B.begin() + j, B.end()), k - j);
    } else {
        // Discard the first i numbers from A, which can never be the kth number
        return findKthElement(vector<int>(A.begin() + i, A.end()), B, k - i);
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = A.size();
    return findKthElement(A, B, n);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 由于这里进行了数组复制，所以空间复杂度为 。

个人评分：12 分，主体思路正确，时间复杂度为最优，空间复杂度可以优化，没有利用两个数组等长和中位数这一条件，可以继续优化。

方法六：二分查找变体优化

由于两个数组长度相等，且寻找中位数，方法五可以进行优化。二分查找本质是保留一部分，舍弃一部分，方法五只对其中一个数组应用该思想，本方法对两个数组均应用该思想。

两个有序数组分别是 和 。要找到第 个元素，我们可以比较 和 。

由于 和 的前面分别有 和 ，即各有 个元素，对于 ，

若 为奇数，则 ，最多只会有 个元素比它小，也就是 最多恰为第 小的数，这里先假设 ，则 （等价于 ）都小于或等于 ，可以直接排除。

若 为偶数，则 ，最多只会有 个元素比它小，也就是 最多恰为第 小的数，这里先假设 ，则 （等价于 ）都小于或等于 ，可以直接排除。

由于 和 的后面分别有 和 ，即各有 个元素，对于 ，因为 最多只会有 个元素比它大，也就是 最少恰为第 小的数，这里先假设 ，则 （等价于 ）都大于或等于 ，可以直接排除。

因此我们可以归纳出三种情况：

• 情况一： ，排除 和 ，同时缩小 为 。
• 情况二： ，排除 和 ，同时缩小 为 。
• 情况三： ，归纳为情况一或者情况二。

其实我们可以对情况三进行进一步讨论，此时设 。

若 为奇数，此时恰有 个元素小于或等于 ，且恰有 个元素大于或等于 ，取 或 放入大于或等于 的集合，则恰有 个元素小于或等于 ，且恰有 个元素大于或等于 ，则 为中位数，可以直接返回。

若 为偶数，此时恰有 个元素小于或等于 ，且恰有 个元素大于或等于 ，取 或 放入小于或等于 的集合，则恰有 个元素小于或等于 ，且恰有 个元素大于或等于 ，则 为中位数，可以直接返回。

因此三种情况可以优化为：

• 情况一： ，排除 和 ，同时缩小 为 。
• 情况二： ，排除 和 ，同时缩小 为 。
• 情况三： ，直接返回 。

递归调用上述过程，终止情况：

• ，返回两个数组仅剩余两个元素中的最小值。

因为 ，所以不会越界。

优化前（方法五）每次迭代后两个数组中最多只有一个数组能够缩减一段。

优化后（方法六）每次迭代后两个数组中每个数组都能缩减一段，每个数组的数据规模缩小为原来的一半（向上取整），加速了代码进程。

画出有向图，→指向表示有向边，有向边起点元素小于或等于有向边终点元素。

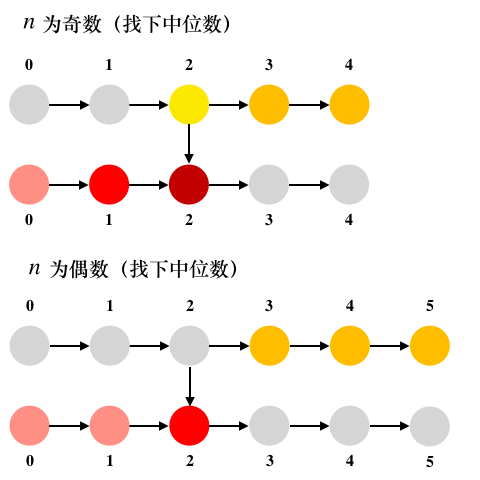
如上图，灰色结点淘汰。

递归版本一，保存下标，为原地算法。这里总共有五个变量， 两个数组的首尾元素下标合计 4 个，数组长度一个，由于 ，我们只记录 首个元素下标 ， 首个元素下标 ，和数组长度 。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findMedian(int *a, int *b, int n, int pa, int pb) {
    if (n == 1) {
        return min(a[pa], b[pb]);
    }
    int ma = pa + (n + 1) / 2 - 1;
    int mb = pb + (n + 1) / 2 - 1;
    if (a[ma] < b[mb]) {
        return findMedian(a, b, (n + 1) / 2, pa + n / 2, pb);
    } else if (a[ma] > b[mb]) {
        return findMedian(a, b, (n + 1) / 2, pa, pb + n / 2);
    } else {
        return a[ma];
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findMedian(A, B, n, 0, 0);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedian(vector<int>& A, vector<int>& B, int pa, int pb, int n) {
    if (n == 1) {
        return min(A[pa], B[pb]);
    }
    int ma = pa + (n + 1) / 2 - 1;
    int mb = pb + (n + 1) / 2 - 1;
    if (A[ma] < B[mb]) {
        return findMedian(A, B, pa + n / 2, pb, (n + 1) / 2);
    } else if (A[ma] > B[mb]) {
        return findMedian(A, B, pa, pb + n / 2, (n + 1) / 2);
    } else {
        return A[ma];
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = (int)A.size();
    return findMedian(A, B, 0, 0, n);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：15 分，主体思路正确，时间复杂度和空间复杂度均为最优。

递归版本二，这里不保存下标，直接进行数组复制，参数更少，写法更加简单一点。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findMedian(int *a, int *b, int n) {
    if (n == 1) {
        return min(a[0], b[0]);
    }
    if (a[(n + 1) / 2 - 1] < b[(n + 1) / 2 - 1]) {
        int na[(n + 1) / 2];
        for (int t = 0; t < (n + 1) / 2; ++t) {
            na[t] = a[t + n / 2];
        }
        return findMedian(na, b, (n + 1) / 2);
    } else if (a[(n + 1) / 2 - 1] > b[(n + 1) / 2 - 1]) {
        int nb[(n + 1) / 2];
        for (int t = 0; t < (n + 1) / 2; ++t) {
            nb[t] = b[t + n / 2];
        }
        return findMedian(a, nb, (n + 1) / 2);
    } else {
        return a[(n + 1) / 2 - 1];
    }
}
 
int findMedianSortedArrays(int *A, int *B, int n) {
    return findMedian(A, B, n);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedian(vector<int> A, vector<int> B, int n) {
    if (n == 1) {
        return min(A[0], B[0]);
    }
    if (A[(n + 1) / 2 - 1] < B[(n + 1) / 2 - 1]) {
        return findMedian(vector<int>(A.begin() + n / 2, A.end()), vector<int>(B.begin(), B.begin() + n - n / 2), (n + 1) / 2);
    } else if (A[(n + 1) / 2 - 1] > B[(n + 1) / 2 - 1]) {
        return findMedian(vector<int>(A.begin(), A.begin() + n - n / 2), vector<int>(B.begin() + n / 2, B.end()), (n + 1) / 2);
    } else {
        return A[(n + 1) / 2 - 1];
    }
}
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = (int)A.size();
    return findMedian(A, B, n);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 由于这里进行了数组复制，所以空间复杂度为 。

个人评分：14 分，主体思路正确，时间复杂度为最优，空间复杂度可以优化。

迭代版本一，保存下标，为原地算法。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findMedianSortedArrays(int *a, int *b, int n) {
    int pa = 0, pb = 0, ma, mb;
    while (n > 1) {
        ma = pa + (n + 1) / 2 - 1;
        mb = pb + (n + 1) / 2 - 1;
        if (a[ma] == b[mb]) return a[ma];
        if (a[ma] < b[mb]) {
            pa += n / 2;
        } else {
            pb += n / 2;
        }
        n = (n + 1) / 2;
    }
    return min(a[pa], b[pb]);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    int n = (int)A.size();
    int pa = 0, pb = 0, ma, mb;
    while (n > 1) {
        ma = pa + (n + 1) / 2 - 1;
        mb = pb + (n + 1) / 2 - 1;
        if (A[ma] == B[mb]) return A[ma];
        if (A[ma] < B[mb]) {
            pa += n / 2;
        } else {
            pb += n / 2;
        }
        n = (n + 1) / 2;
    }
    return min(A[pa], B[pb]);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

• 时间复杂度： 。
• 空间复杂度： 。

个人评分：15 分，主体思路正确，时间复杂度和空间复杂度均为最优。

王道论坛出版的《计算机专业基础综合考试历年真题解析》或高等教育出版社出版的《全国硕士研究生招生考试计算机学科专业基础考试大纲》给的参考答案就是本方法的迭代写法，参考答案保存了首尾元素下标共计 4 个变量，并且分奇偶情况讨论，这版代码相比本人提供代码复杂一些。本人摘录如下，方便同学们自行对比。

C 代码如下（含测试用例）：

#include <stdio.h>
 
int min(int x, int y) {
    return x < y ? x : y;
}
 
int findMedianSortedArrays(int *A, int *B, int n) { // n即为序列长度L
    int s1 = 0, e1 = n - 1, mid1, s2 = 0, e2 = n - 1, mid2;
    while(s1 != e1 || s2 != e2) {
        mid1 = (s1 + e1) / 2;
        mid2 = (s2 + e2) / 2;
        if (A[mid1] == B[mid2]) {
             return A[mid1];
        } else if (A[mid1] < B[mid2]) {
            // 分别考虑奇数和偶数，保持两个子数组元素个数相等
            if ((s1 + e1) % 2 == 0) { // 若元素个数为奇数
                 s1 = mid1;  // 舍弃A中间点以前的部分
                 e2 = mid2;  // 舍弃B中间点以后的部分
            } else { // 若元素个数为偶数
                 s1 = mid1 + 1;  // 舍弃A中间点及中间点以前的部分
                 e2 = mid2;  // 舍弃B中间点以后的部分
            }
        } else {
            // 分别考虑奇数和偶数，保持两个子数组元素个数相等
            if ((s1 + e1) % 2 == 0) { // 若元素个数为奇数
                 e1 = mid1;  // 舍弃A中间点以后的部分
                 s2 = mid2;  // 舍弃B中间点以前的部分
            } else { // 若元素个数为偶数
                 e1 = mid1;  // 舍弃A中间点以后的部分
                 s2 = mid2 + 1;  // 舍弃B中间点及中间点以前的部分
            }
        }
    }
    return min(A[s1], B[s2]);
}
 
int main() {
    int s1[] = {11, 13, 15, 17, 19};
    int s2[] = {2, 4, 6, 8, 20};
    printf("%d", findMedianSortedArrays(s1, s2, 5));
    return 0;
}

C++ 代码如下（含测试用例）：

#include <iostream>
#include <vector>
using namespace std;
 
int findMedianSortedArrays(vector<int>& A, vector<int>& B) {
    const int n = A.size();
    int s1 = 0, e1 = n - 1, mid1, s2 = 0, e2 = n - 1, mid2;
    while(s1 != e1 || s2 != e2) {
        mid1 = (s1 + e1) / 2;
        mid2 = (s2 + e2) / 2;
        if (A[mid1] == B[mid2]) {
             return A[mid1];
        } else if (A[mid1] < B[mid2]) {
            // 分别考虑奇数和偶数，保持两个子数组元素个数相等
            if ((s1 + e1) % 2 == 0) { // 若元素个数为奇数
                 s1 = mid1;  // 舍弃A中间点以前的部分
                 e2 = mid2;  // 舍弃B中间点以后的部分
            } else { // 若元素个数为偶数
                 s1 = mid1 + 1;  // 舍弃A中间点及中间点以前的部分
                 e2 = mid2;  // 舍弃B中间点以后的部分
            }
        } else {
            // 分别考虑奇数和偶数，保持两个子数组元素个数相等
            if ((s1 + e1) % 2 == 0) { // 若元素个数为奇数
                 e1 = mid1;  // 舍弃A中间点以后的部分
                 s2 = mid2;  // 舍弃B中间点以前的部分
            } else { // 若元素个数为偶数
                 e1 = mid1;  // 舍弃A中间点以后的部分
                 s2 = mid2 + 1;  // 舍弃B中间点及中间点以前的部分
            }
        }
    }
    return min(A[s1], B[s2]);
}
 
int main() {
    vector<int>s1 = {11, 13, 15, 17, 19};
    vector<int>s2 = {2, 4, 6, 8, 20};
    cout << findMedianSortedArrays(s1, s2);
    return 0;
}

时间复杂度： 。

空间复杂度： 。

个人评分：15 分，主体思路正确，时间复杂度和空间复杂度均为最优。

总结

方法总结

这道题的难度非常大，思维难度相当高，《算法导论》练习题难度都不低，力扣原题也标记为困难题，这个标记是没有任何问题的。

方法一到方法六思路上是层层递进关系，官方题解直接给出的是方法六，也是本题的最优解。

• 本题最优解为方法六，网上能搜到的历年真题参考答案与王道论坛出版的《计算机专业基础综合考试历年真题解析》中的参考答案与之类似，但是都没出解题步骤，我在这里给出详细推导，时间复杂度 ，空间复杂度 。（个人评分 15 分）
• 次优解为方法三、方法四，与《算法导论》的教师手册_Instructor’s Manual for Introduction to Algorithms (Third Edition)_ 提供的官方题解类似，但是引入了边界值，时间复杂度 ，空间复杂度 。（个人评分 14 分）
• 中等解为方法五。时间复杂度 ，但是此方法时间复杂度隐藏因子大于最优解时间复杂度隐藏因子，空间复杂度 。（个人评分 13 分）
• 较差解为方法二。套用了有序数组第 K 小问题模板，时间复杂度 ，其中 为数组值域大小。空间复杂度 。（个人评分 10 分）
• 最差解为方法一。时间复杂度 ，空间复杂度 。（个人评分 8 分）

按照 408 评分标准，哪怕你用的是朴素解（暴力解），也能得到大约一半分。

我们看下力扣官方题解下的最高赞点评：

我差点笑出了猪叫，哎，应该是苦笑，生不出人，我很抱歉，考不上研，我真垃圾！我有时候也在想，考研是为了什么，仅仅是为了一张文凭好得到世俗的认可？不，我们都是活生生的人，作为一个人，就要有人的意志和尊严！战吗？战啊！以最卑微的梦， 致那黑夜中的呜咽与怒吼！

考点总结

这道题的命题组的想考察的是《算法导论》第九章知识点顺序统计量，以及《算法导论》第四章知识点分治法。

二分查找为分治法最经典的应用之一，常用的排序算法归并排序和快速排序也应用了分治法。

相关章节如下：

• 算法导论（第四版）第二章：入门　第三节：设计算法
• 算法导论（第四版）第四章：分治法　前言
• 算法导论（第四版）第九章：中位数和顺序统计量　前言

2022 年全国硕士研究生招生考试计算机科学与技术联考计算机学科专业基础综合试题题 42 也对顺序统计量进行了考察，为无序数组第 K 小问题，直接套用无序数组第 K 小问题模板即可。2022 年距离 2011 年已经过去了 11 年，《算法导论》知识点在 408 中基本上是 5-10 年考察一次，基本属于超纲内容，所以同学们也没必要过分担心，基础分拿到手就行。

拓展

本题也可以进行拓展。

拓展一

改成求两个长度均为 的有序数组的上中位数。可以有两种思路。

• 思路一：找第 大的数。
• 思路二：找第 小的数。

以上六种解法仍然适用。

拓展二

改成如果两个数组长度分别为 和 ，找出这两个数组中第 小的数。

前五种解法仍然适用，最后一种解法只能对两个相同长度的数组同时缩放，就行不通了。

寄语

可以看出，408 有些题的最优解都是特解，非常强调技巧性。类似的还有：

• 2013 年第 41 题，最优解为摩尔投票算法。
• 2018 年第 41 题，最优解为原地哈希。
• 2020 年第 41 题，最优解为指针数组。

这种特解题除了平时多积累，别无他法。

这种题命题组就是用来拉区分度的，基本就是冲击 130+，140 + 的拦路虎，考场上想不出来也不要过分自责影响心态，你做不出来别的考生大概率也做不出来，所以心态一定要好，考场上要以尽量多拿分为目标，如果真的很不幸这一年的算法题为困难题，暴力解先保分吧！

最后祝大家 2023 考研顺利！