题12
题目
[!question]+
设函数
分析
[!NOTE]+
又是偏积分的考点,这回还是没积出来,算是阴差阳错算对了,可以考虑先对x积出来原函数,再对y偏导,建立

第二做的时候,没注意到这里还有一个偏导数相等的方程,想着说怎么少一个方程
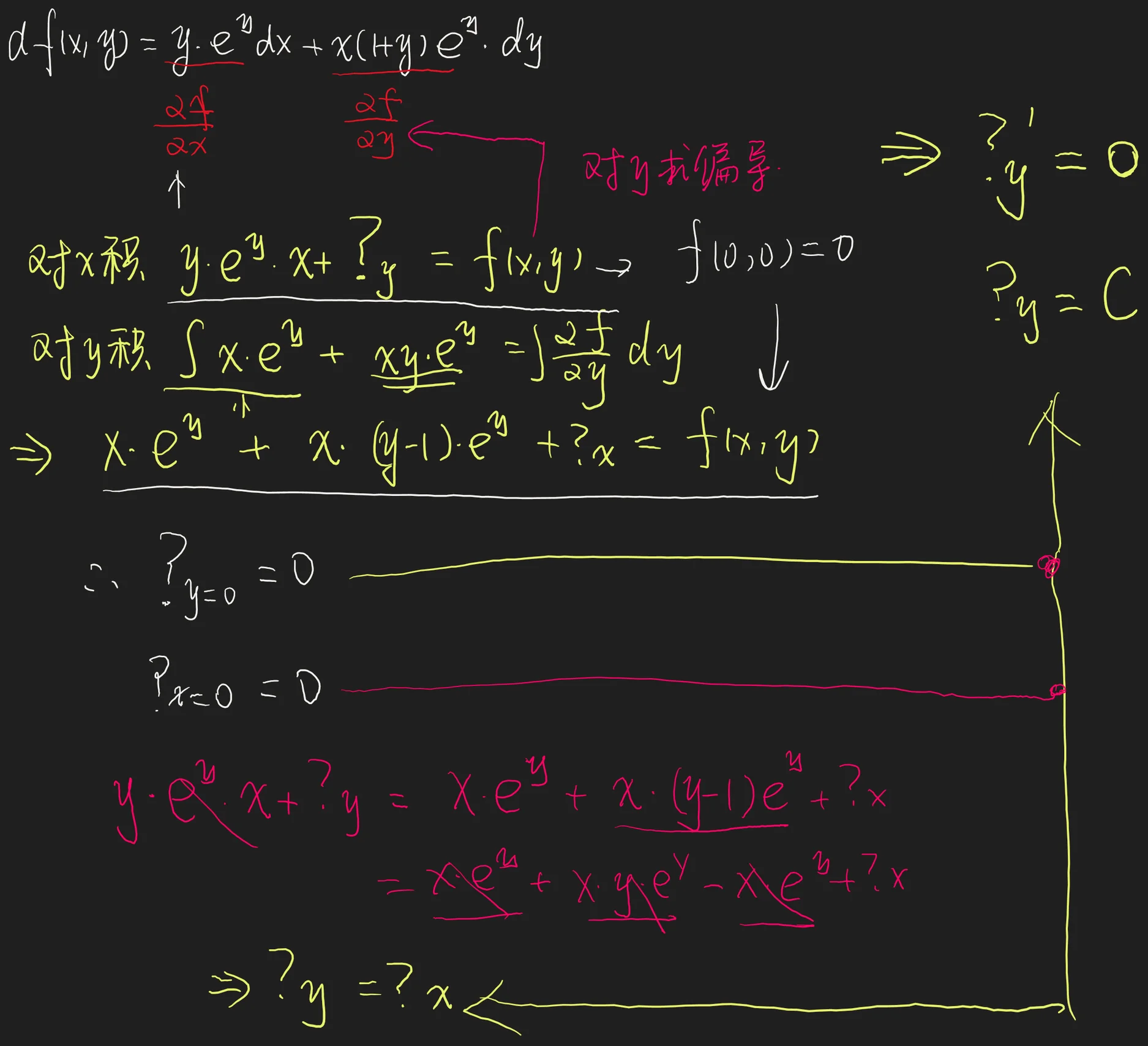
解
[!done]-
解 由于
故
对
其中
对
与
代入
注 本题也可以利用凑微分法求解.
由于
设
Jun 19, 20252 min read
[!question]+
设函数
[!NOTE]+
又是偏积分的考点,这回还是没积出来,算是阴差阳错算对了,可以考虑先对x积出来原函数,再对y偏导,建立

第二做的时候,没注意到这里还有一个偏导数相等的方程,想着说怎么少一个方程
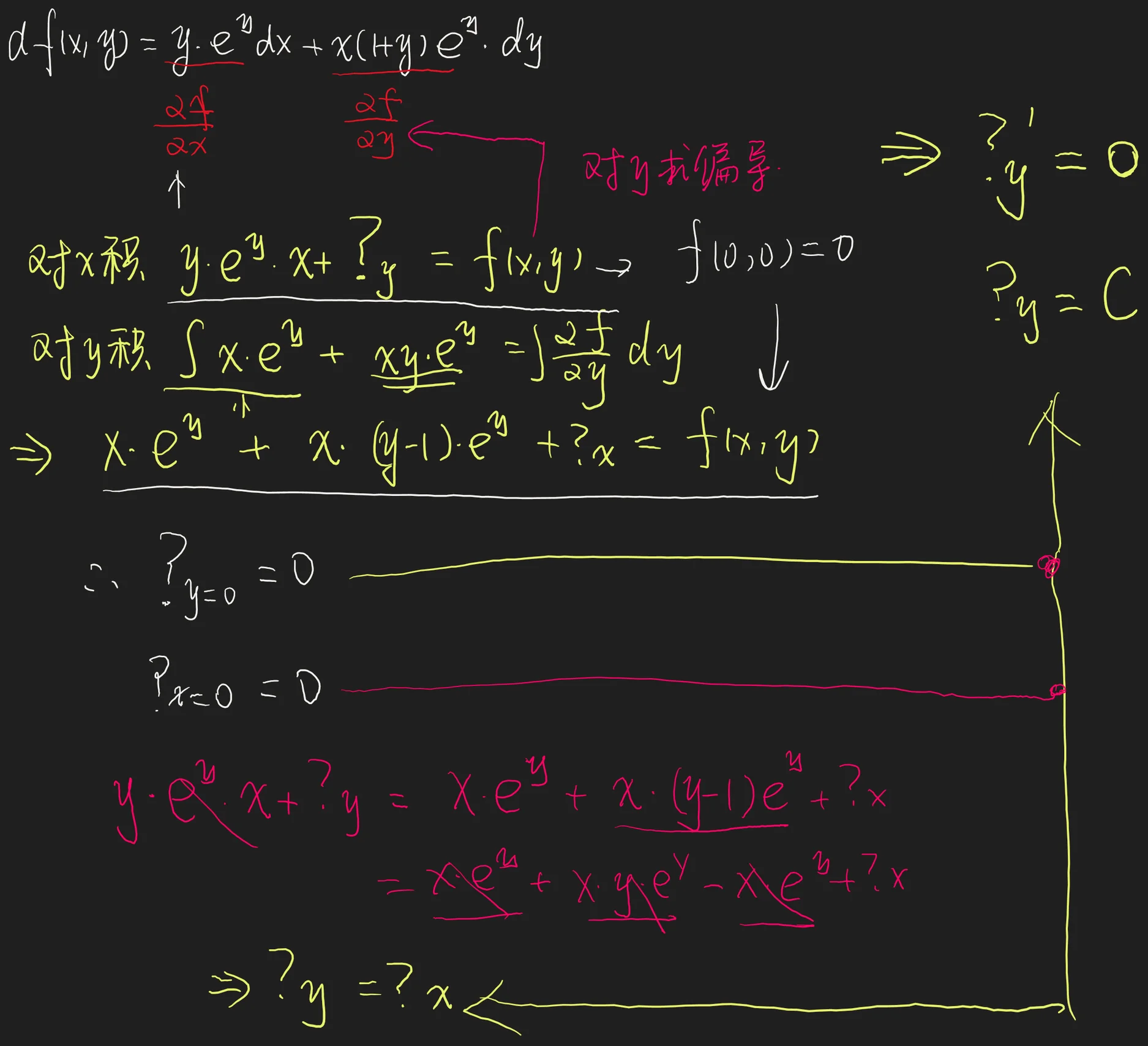
[!done]-
解 由于
故
对
其中
对
与
代入
注 本题也可以利用凑微分法求解.
由于
设