例4.4
题目
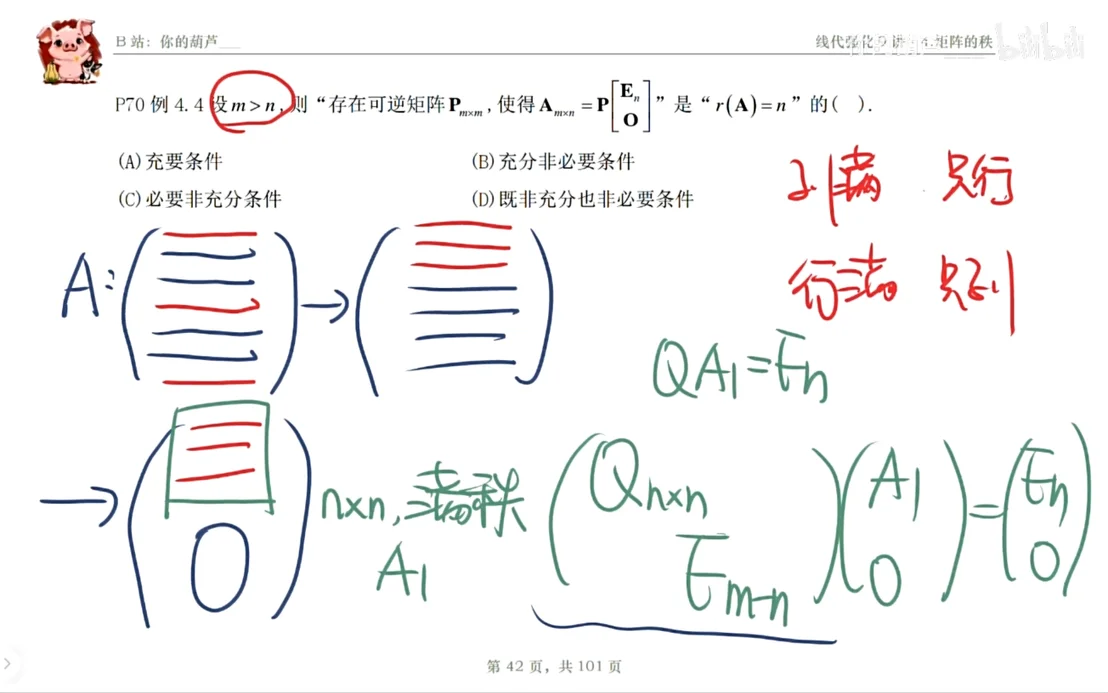
P70 设
(A) 充要条件
(B) 充分非必要条件
(C) 必要非充分条件
(D) 既非充分也非必要条件
分析
矩阵乘上可逆矩阵,矩阵的秩是不变的,而左右两边又是相等的,所以这个结论是充分的
说明必要性,任何一个矩阵,都可以通过初等变换中的行和列变化,得到它的标准形,也就
解
【解】应选 (A).
若
令
又当
【注】若
P70 设
(A) 充要条件
(B) 充分非必要条件
(C) 必要非充分条件
(D) 既非充分也非必要条件
矩阵乘上可逆矩阵,矩阵的秩是不变的,而左右两边又是相等的,所以这个结论是充分的
说明必要性,任何一个矩阵,都可以通过初等变换中的行和列变化,得到它的标准形,也就
【解】应选 (A).
若
令
又当
【注】若
