本文将罗列一元函数积分学中的一些技巧与公式, 只挑了我认为最重要的, 必须牢记的.
首先, 叩拜大纲.

区间再现换元
证明思路: 做换元
从几何上看, 相当于把从左到右的定积分换成从右到左的定积分.
对称区间上的定积分
证明思路: 对左半区间做镜像换元即可.
对于奇函数, 上式为 0. 对于偶函数, 上式为对半区间积分的 2 倍.
此外, 容易验证以下函数的
这些形式的函数要牢记, 我记得老高考题喜欢考这些玩意, 莫名的怀念啊.
周期函数的定积分
证明思路: 将右式的积分区间拆分, 做平移换元即可.
推论:
证明思路: 左式等分成 n 个区间相加即为右式.
三角函数的定积分
三角函数的定积分用到的技巧是最多的.
1. 华里士公式 / 点火公式 (Wallis’ integrals)
证明思路: 使用分部积分得到递推式, 递归导出通项.
2. 正交性
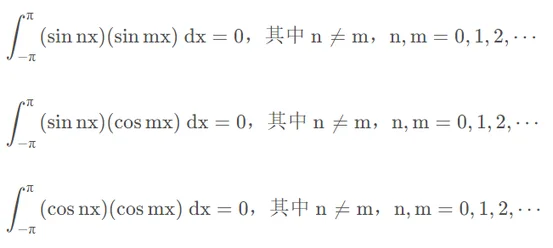
证明思路: 对被积函数使用积化和差变形.
3. 对称性
三角函数的对称性衍生出了一卡车的性质.
证明思路: 使用区间再现换元.
证明思路: 使用区间再现换元.
证明思路: 对后半区间做平移换元.
证明思路: 对后半区间做平移换元, 然后使用华里士公式.
证明思路: 对后半区间做平移换元, 然后综合使用刚才介绍过的公式.
Gamma 函数
导出思路: 可由正态分布的概率密度函数性质导出.
证明思路: 使用分部积分得到递推式, 递归导出通项.
此外, 对于形如
反常积分敛散性判别
对于被积函数形如
当
当
当
证明思路: 使用反常积分敛散性的比较判别法, 取 p 积分作为被比较函数, 选取合适的 p 值即可.