第二步:对真分式的分母进行因式分解
首先,实系数多项式因式分解定理告诉我们,一个多项式可以被分解为若干个一次因式 和若干个二次因式 相乘。即一个多项式,可以分解为以下四种因子:
如果真因式 中的分母 属于上面四种情况之一,那么我们就直接完成了分母的因式分解。如果不是,那么 就是一个三次方以上的多项式,我们就要想办法把这个多项式分解为以上四种因子。
因式分解也是一个求根问题,如果它分解后的根不是整数,一般会比较复杂,特别是高次幂的多项式分解。对于这些问题,可以通过画图像等其他方式解决。因式分解是另一个数学问题,有一点超出讨论范围了,所以我们不打算深入讨论。我们只讲一讲在解题过程中,进行快速地因式分解的思路。
解题时之所以能够快速因式分解,其实是出题人保证了它可以被快速分解。
设我们要分解一个四次方的多项式:
有些人可能会说, 前面有一个系数 ,最后分解出来的因子能符合上面四种因子吗?其实我们只要把 ,提取掉变成 就行了,这是完全不影响我们之前的结论的。
先设这个多项式可以分解为两个因子,其中一个为线性式 :
在试题中,系数通常是整数。即 应该可以整除 ,而 可以整除 。这样我们就把 和 限定在比较小的范围内了。
例如,分解:
,因子为1, 2; 的因子为1, 2, 3, 4, 6, 12, 24以及它们的负数。
我们先尝试选择 ,使用分式除法验证能不能被式子整除:

有余数,因此不能整除。同样的 也不可以, 可以:

即
现在就变成对 进行因式分解。,因子为1, 2。 的因子现在只有1, 2, 3, 4, 6以及它们的负数。
我们同样可以找到因子 :
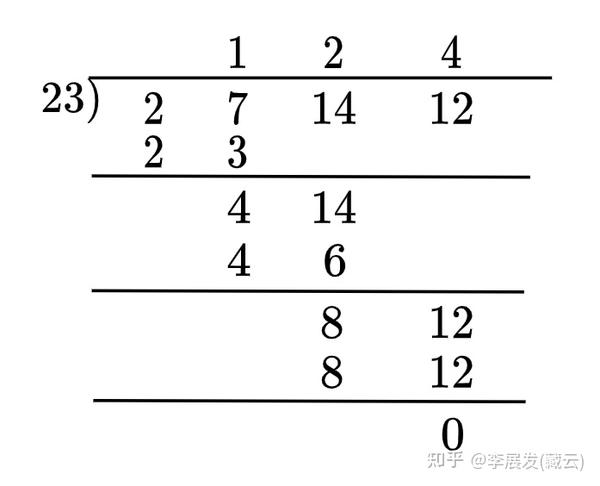
即:,显然 已经不能再约分,因此分解结束。
如果任何 都无法整除我们要分解的式子,那么就证明这个式子的所有因子都是形如 的,重复上面的方法,找到 的因子即可。


