题12

题12

题目

具有 51 个顶点和 21 条边的无向图的连通分量最多为 ( ).
A. 33
B. 34
C. 45
D. 32

分析

连通分量是一个极大连通图，子图必须是一个完全无向图
而一个完全无向图的结点如果是n，那么边就有，根据题目，这里的边比较少，我们就以边为核心来计算

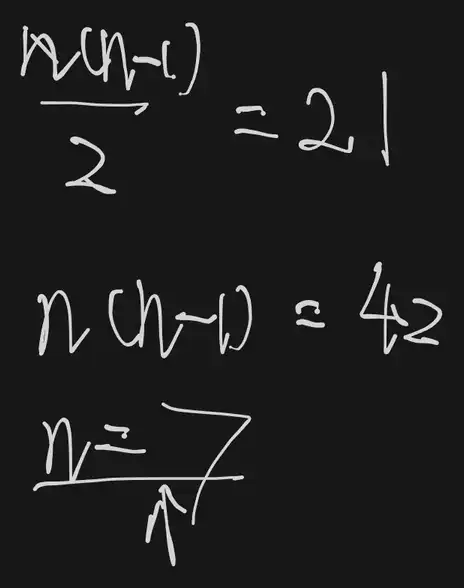
还剩下了51-7=44个结点，也就是这个一共构成了44个子图，每一个都是连通分量，同时保证了最多

解

C
初始考虑只有 51 个顶点的无向图 ,此时 中每个顶点都是连通分量,问题转化为向 中添加 21 条边, 如何添加这 21 条边使得连通分量数目最多。
若向两个不同的连通分量之间添加边, 则连通分量数目会减 1 , 所以应尽可能地将这 21 条边加入同一个连通分量且让其接近完全图, 含有 7 个顶点的完全图有 21 条边, 所以用 7 个顶点构成一个含有 21 条边的连通分量, 剩下 个顶点对应 44 个连通分量,共有 45 个连通分量。