jordan标准型

在复习用书、模拟卷中，经常会出现形如

的矩阵，特征是在对角线上方或下方出现若干个 1. 这样的矩阵与对角阵只有一个 1 的区别，在命题过程中经常出现.

完整的标准型理论比较复杂.本期视频在考研数学范围内来解释若尔当标准型在相似理论中起怎样的作用以及所涉考查方法.

若能按照 “” 这种相似关系进行分类，每一类里面两个个体都有这种关系，来自不同类的个体不具有这种关系。则这种关系需要满足以下三点：

满足三种关系即可称之为等价关系，按照等价关系分的类叫做等价类。矩阵的相似关系就是等价关系.

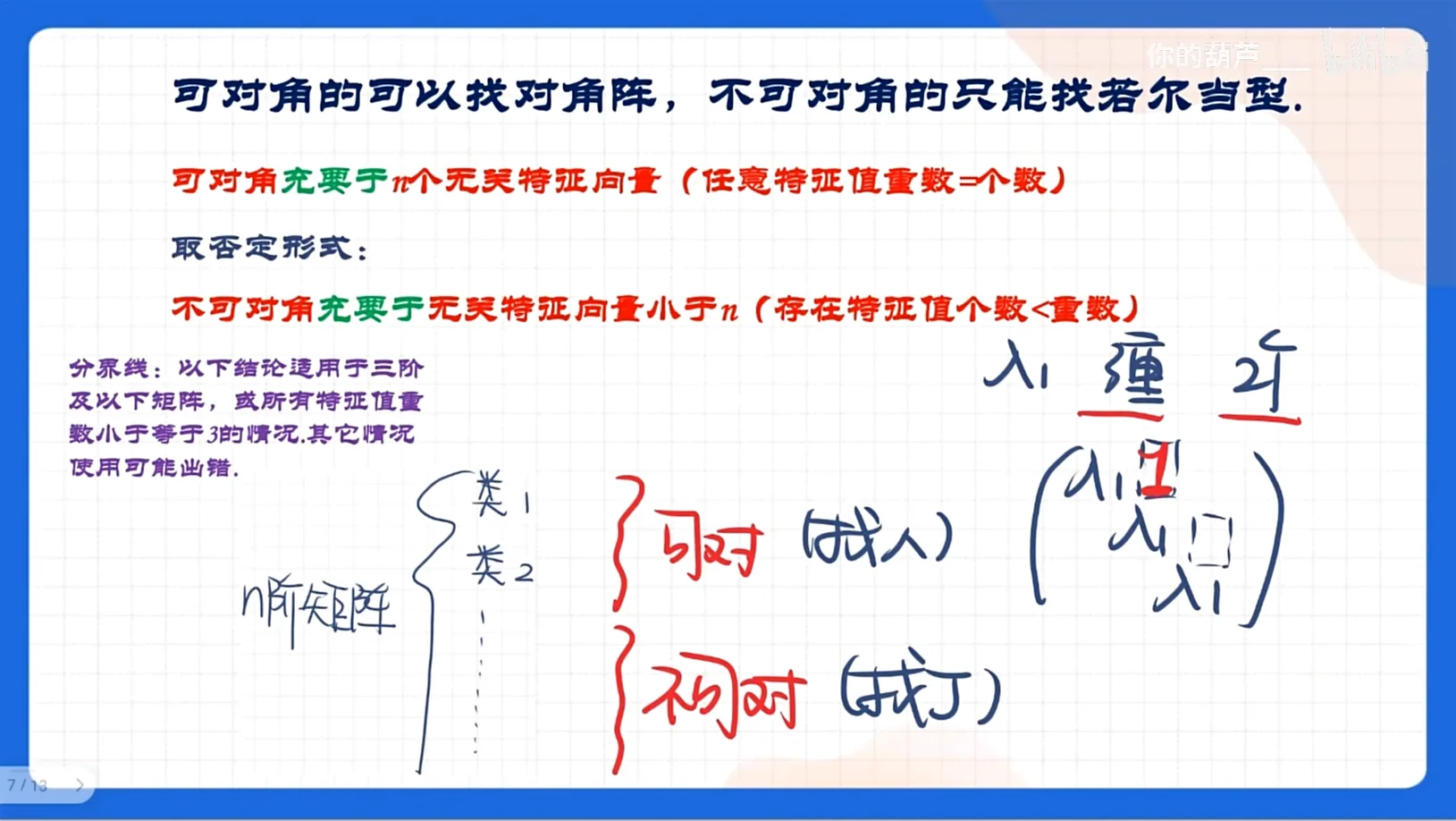
可对角化的矩阵可以找对角阵作为代表元，不可对角化的矩阵只能找若尔当标准型作为代表元.

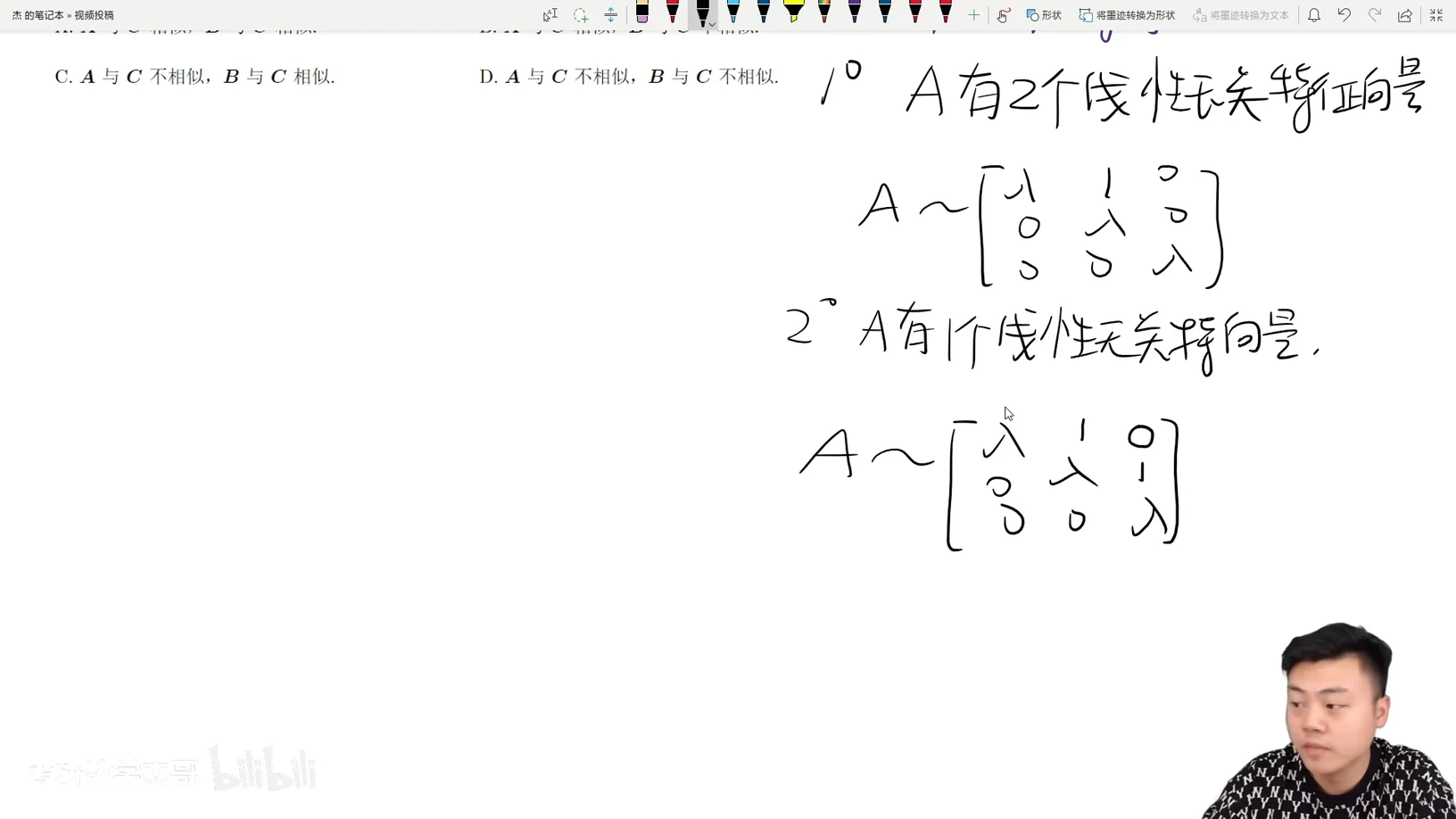
可对角化充要条件是存在个线性无关的特征向量（任意特征值重数=个数）

最容易考察的考点：

不可对角化充要条件是线性无关的特征向量个数小于（存在某个特征值的几何重数小于代数重数）

分类策略：以下结论适用于三阶及以下矩阵，或所有特征值的代数重数小于等于 3 的情况。其它情况或许可用也或许不可用.

阶矩阵

类 类 可 对 角 化 找 对 角 阵 不 可 对 角 化 找 若 尔 当 标 准 型

主对角线上补了几个1就意味着缺几个特征向量

矩阵相似，无论能否对角化，只要看它们有没有相同的对角矩阵或若尔当标准型，而对角矩阵/若尔当标准型的形状完全由特征值、特征值的重数以及线性无关的特征向量的个数所决定.

故：两矩阵相似充要于特征值相同；特征值的重数相同；对应线性无关的特征向量的个数相同.

别忘了下面这个！！！

结论适用于三阶及以下矩阵，或所有特征值的重数小于等于 3 的情况。其它情况或许可用也或许不可用.

总结：

在阶数 3 阶及以下矩阵或所有特征值的重数小于等于 3 的情况下，若存在某个特征值对应的线性无关的特征向量的个数小于其重数，则该矩阵不可对角化. 且必存在一个与之相似的若尔当标准型.

将特征值排布在对角线上（相同的特征值放在一起），若某个特征值的几何重数比其代数重数少个，就在对应特征值所在对角线的上方或下方随便补个 1.

下列矩阵中，与矩阵相似的为

三重

只有一个线性无关的特征向量

所以答案为 A

2 阶若尔当型求解相似矩阵——直接设矩阵即可

P63 例 3. 20 若 , ，求所有可逆矩阵，使得 .

解：设，则由可得，即

计算可得：

故：

任意.

3 阶若尔当型求解相似矩阵——设矩阵的列

21. (本题满分 12 分)
设矩阵 , .

(1) 能否相似对角化?说明理由:
(2) 是否存在可逆矩阵，使得 ?若存在，求出所有的 . 若不存在，请说明理由.

解：

设，则由可得，即

计算可得：

，但对应的线性无关的特征向量只有一个，所以不能相似对角化.

设，则

由于可逆，所以，即 .

YiNotes