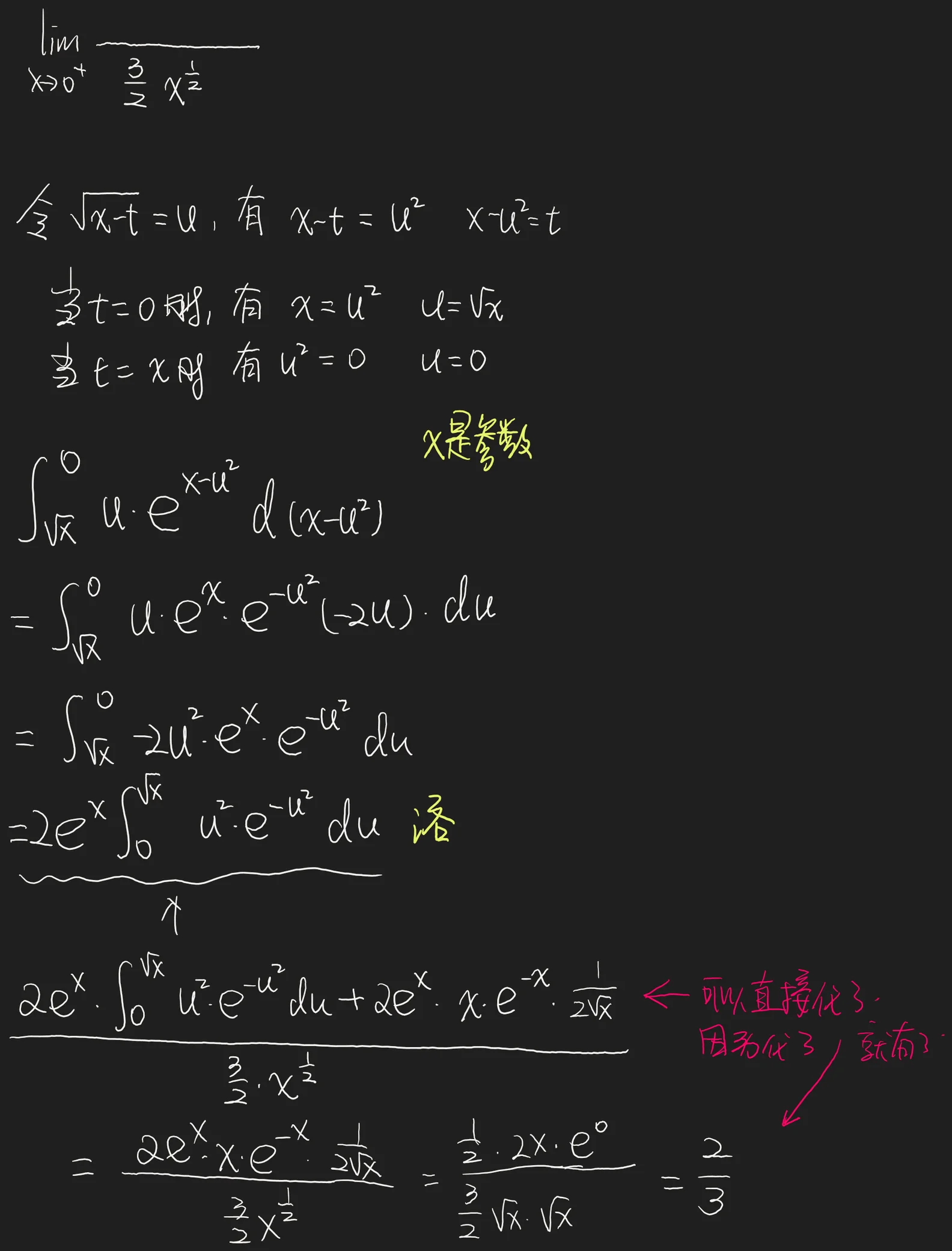题15
题目
[!error]+
求 .
分析
[!NOTE]+
算极限的时候,两个部分乘起来,比如在x趋向于0这里地方,这个例子举得不太好,但是可以体会,左边的我们把x=0带入,得到的应该是1,可以直接带进去。这个题目还涉及了变限积分算极限的问题

下面是第二次做了,算极限,什么时候可以直接带的问题,变限积分夹在在极限里面,题目一般导一次就可以尝试直接带了,应该是不会出现不定式了,不然也太难算了
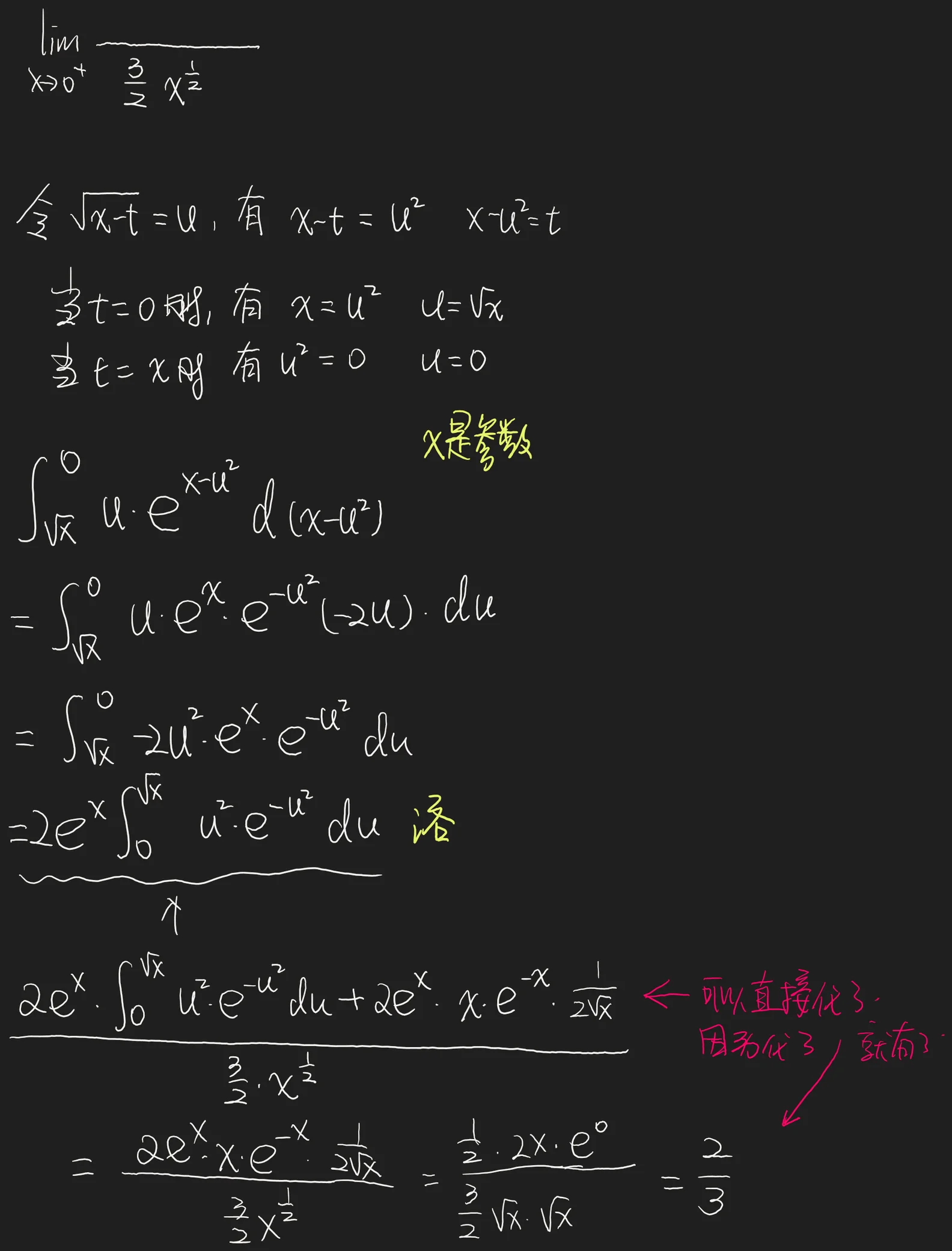
解
[!done]-
原极限是一个 型未定式极限,故可以考虑使用洛必达法则计算.
分子 是一个变限积分,其中 为积分变量, 为参变量,积分限与被积函数中均包含参变量 ,且被积函数中的参变量较难与积分变量分离,因此不能直接利用变限积分的求导公式计算导数.
可以考虑作变量代换 ,将含有 的部分提到积分号外,从而可以利用求导的乘法法则来计算该变限积分的导数.
此外, 也可以利用如下形式的积分中值定理将原极限进行恒等变形, 进而求解.
积分中值定理 若 在 上连续,且 在 上不变号,则
其中 .
解 (法一) 令 ,则 ,
于是,
因此,原极限 .
(法二) 由于 和 均为关于 的连续函数,且 在 上不变号,故由积分中值定理可得,存在 ,使得
因此,
注 本题中的 是以 为参变量 ( 在积分过程中是常量) 的变限积分,并且被积函数中的参变量与积分变量不能 “分离”. 这里的 “分离” 指的是被积函数能写成 的形式. 对于此类积分,一般可以考虑利用变量代换把被积函数写成 的形式.