题17
题目
[!question]+
已知函数
分析
[!NOTE]+

偏积分的考点,求这个无约束极值核心是积分积出来一阶导的函数,求出这个驻点

又做了一遍,基本的思路没有什么问题就是又算错了
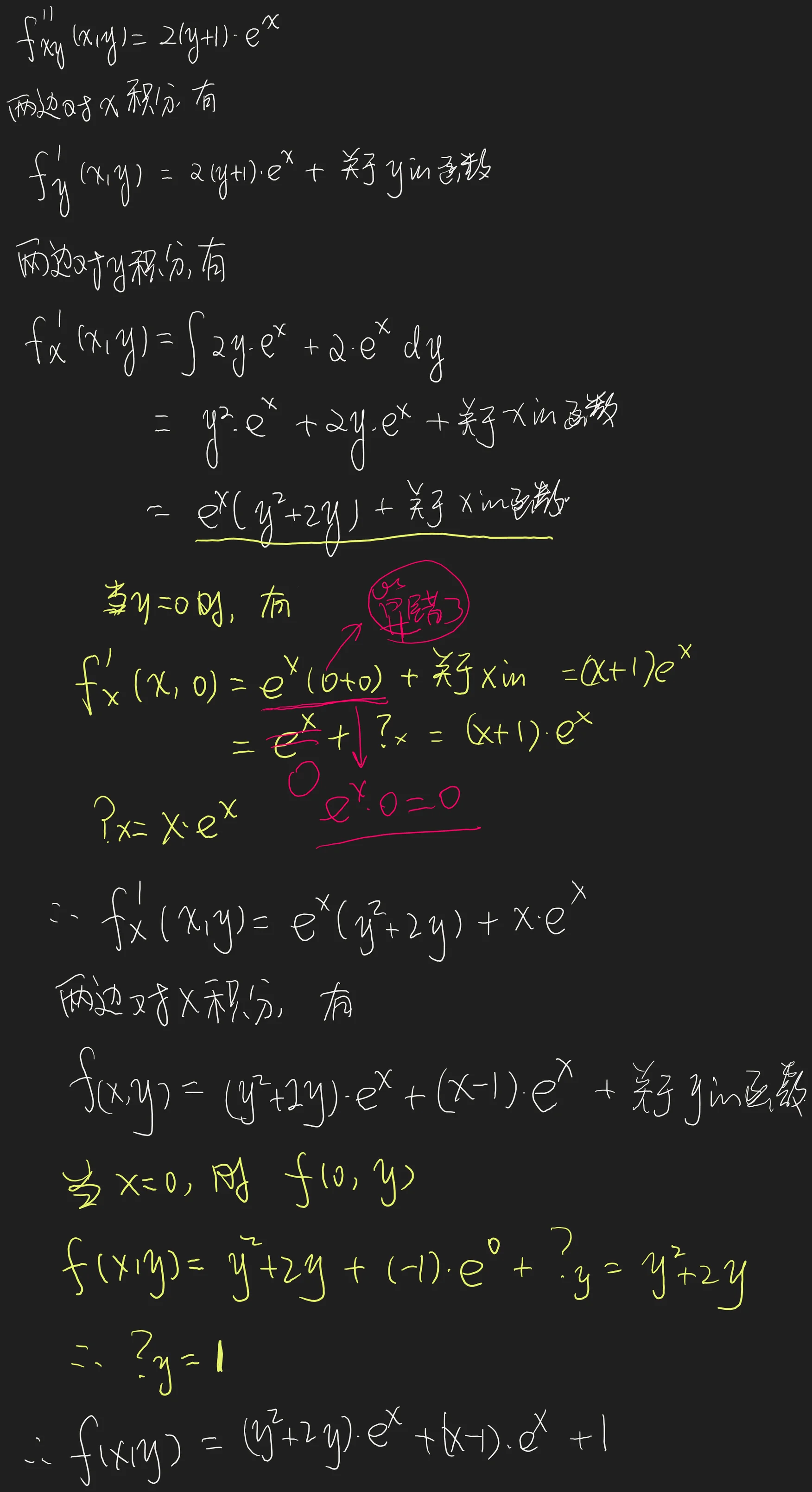
解
[!done]-
已知条件并没有直接给出
解 利用题给条件,我们来逐步求
由于
其中
从而,
其中
因此,
计算
由于
根据二元函数极值存在的充分条件,分别计算
由于
注 本题的关键在于通过求积分来得到
在一元函数的情况下,对
Jun 19, 20253 min read
[!question]+
已知函数
[!NOTE]+

偏积分的考点,求这个无约束极值核心是积分积出来一阶导的函数,求出这个驻点

又做了一遍,基本的思路没有什么问题就是又算错了
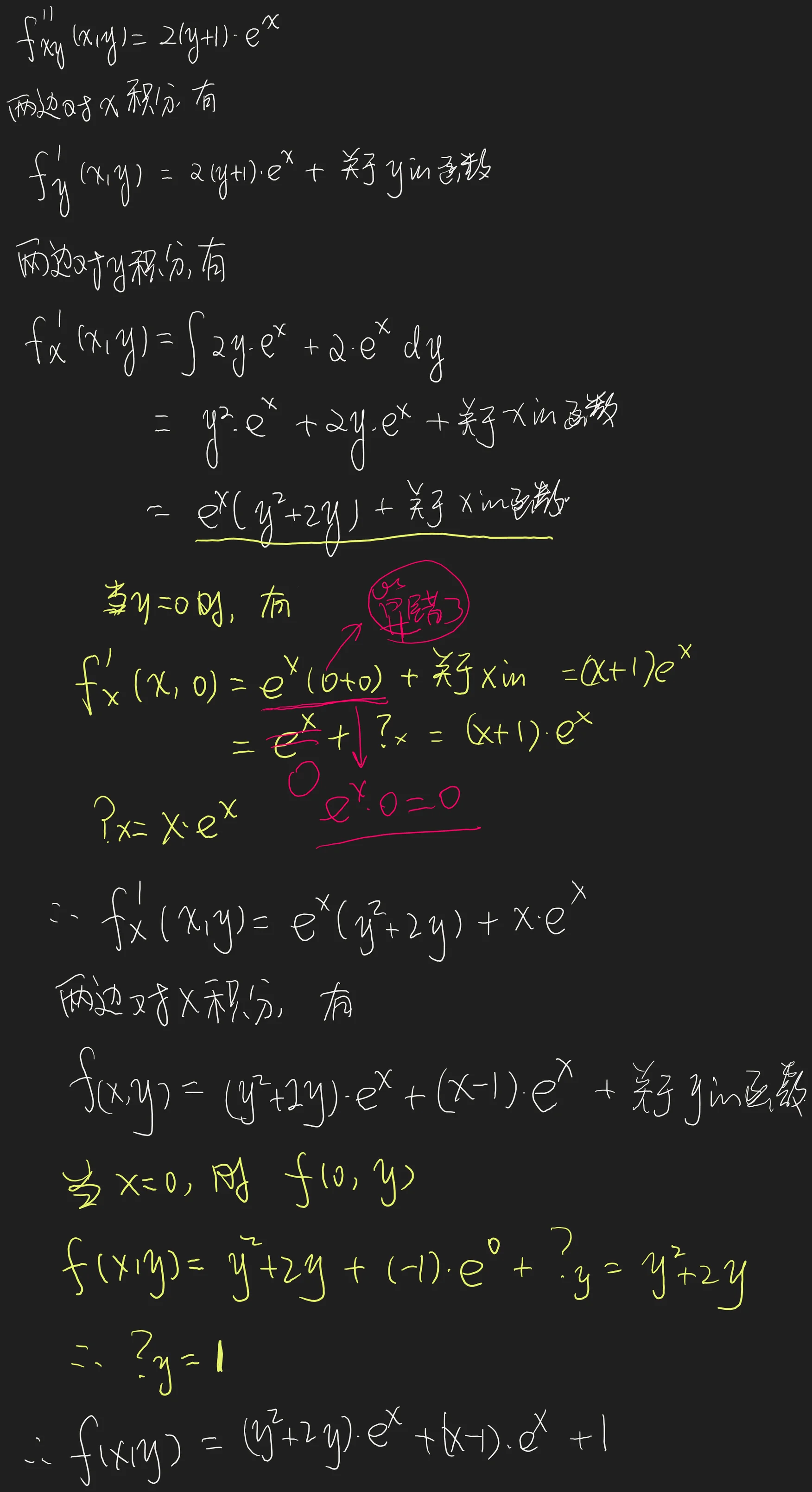
[!done]-
已知条件并没有直接给出
解 利用题给条件,我们来逐步求
由于
其中
从而,
其中
因此,
计算
由于
根据二元函数极值存在的充分条件,分别计算
由于
注 本题的关键在于通过求积分来得到
在一元函数的情况下,对