题17
题目
[!error]+
设平面区域 由曲线 与 轴围成,计算二重积分
分析
[!NOTE]+
本题相当重要
头一次见用参数方程算二重积分,这这里还用到了区间再现公式来简化计算,或者是用形心来处理积分区域关于某个之间x=t或者y=t对称的情况,同时算的又是,另外就是永远记得先定好x和y的范围,然后咔咔描点找出来范围



解
[!done]-
本题中,区域 由摆线的一拱与 轴围成,而摆线方程以参数方程的形式给出,故在计算二重积分时, 应注意积分区域的写法以及参数方程的利用.
解 区域 如图所示. 把区域 看作 型区域, 对应的点
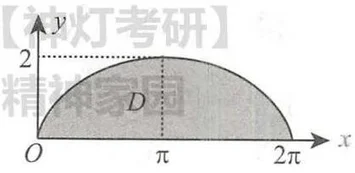
为 对应的点为 对应的点为 ,则
分别计算 和
下面用三种方法计算 .
由于 是关于 的奇函数,故 .
(法二) 由法一知, .
“ ” 处用到了 .
分部积分
分部积分
(法三) 注意到区域 关于直线 对称,故区域 的形心位于该直线上,从而其形心的横坐标 .
根据形心公式, . 于是,
因此, .
注 ① 摆线从 0 到 的一拱可以写成 的形式,但是该函数没有初等函数表达式. 请大家学习本题利用参数方程计算此类区域上的二重积分的方法.
② 法一中利用变量代换将 上的积分转化为对称区间 上的积分,从而可以利用对称性简化计算. 请大家注意这种计算方法.
③ 法三利用了形心坐标计算 ,较为巧妙. 此种计算方法适用于具有某种对称性的区域. 在计算形如 的二重积分时,可以先观察积分区域,判断其是否具有某种对称性,形心坐标是否较易得到. 若通过观察可确定 或 ,则可以利用 或 简化计算.



