题23
题目
[!question]+
已知
( I ) 求
( II ) 求满足
分析
[!NOTE]+
经典的那种解矩阵方程的题目,注意要保证P是可逆的,k1!=k2

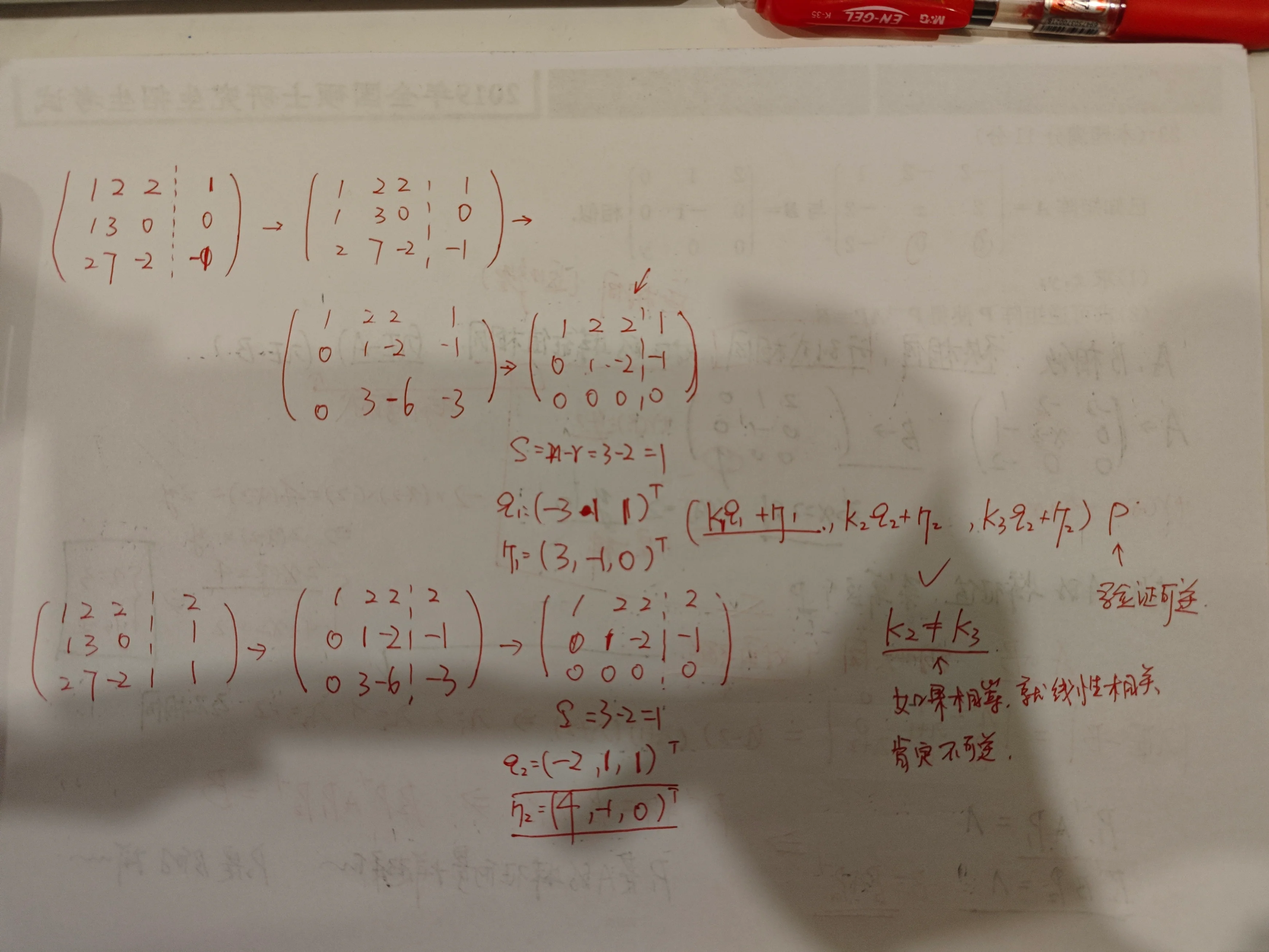
解
[!done]-
由于对矩阵作初等列变换等价于右乘初等矩阵,故已知条件说明矩阵方程
第(II)问可以在第(I)问的结果上计算。求出矩阵方程
(解) (I) 由于
对
当且仅当
或者,由矩阵
因此,
(II) 当
因此,矩阵方程
其中
若可逆矩阵
且
由于
故当
因此,满足
其中
Jun 19, 20255 min read
[!question]+
已知
( I ) 求
( II ) 求满足
[!NOTE]+
经典的那种解矩阵方程的题目,注意要保证P是可逆的,k1!=k2

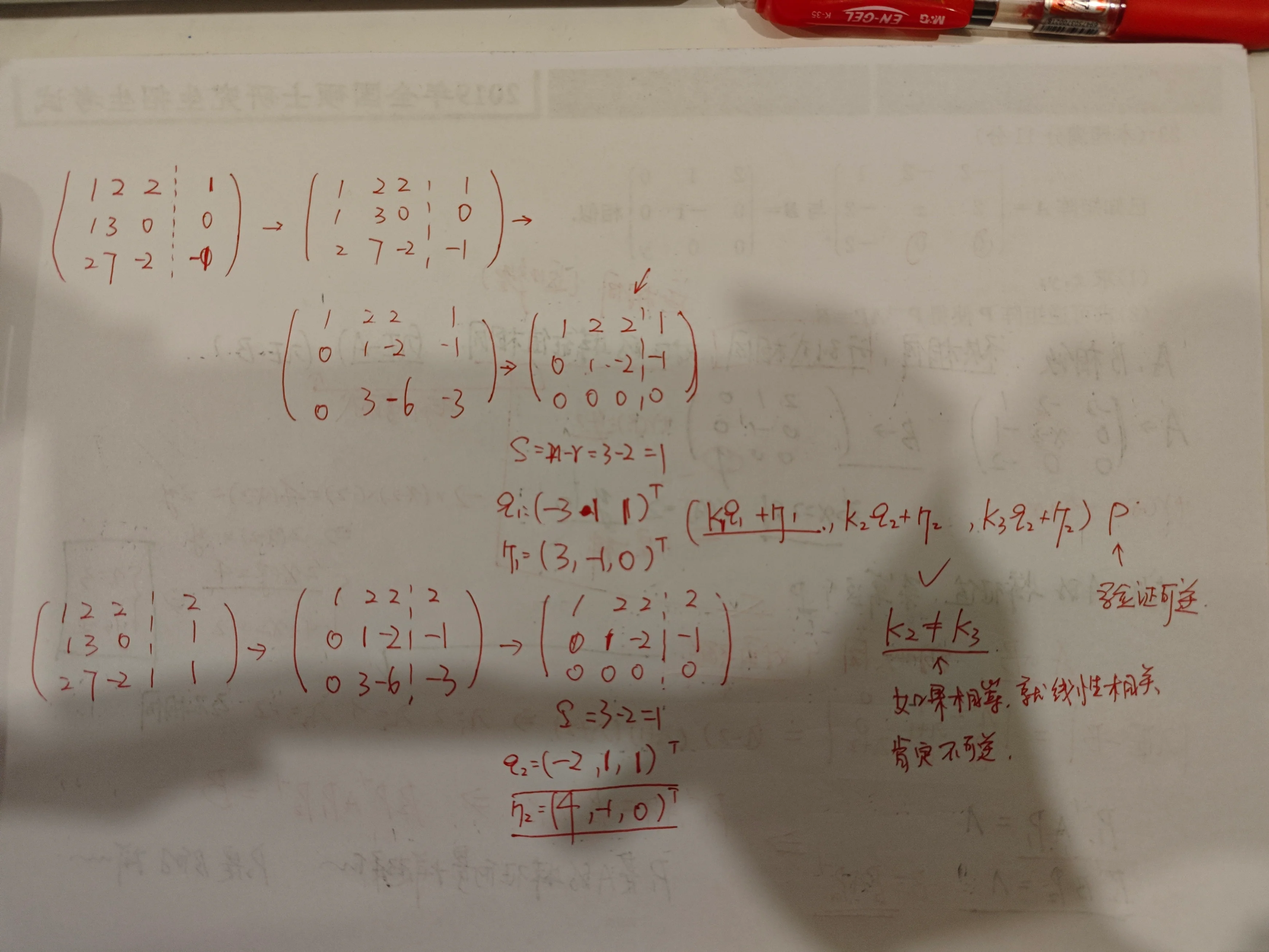
[!done]-
由于对矩阵作初等列变换等价于右乘初等矩阵,故已知条件说明矩阵方程
第(II)问可以在第(I)问的结果上计算。求出矩阵方程
(解) (I) 由于
对
当且仅当
或者,由矩阵
因此,
(II) 当
因此,矩阵方程
其中
若可逆矩阵
且
由于
故当
因此,满足
其中