题18
题目
[!question]+
设
分析
[!NOTE]+
二重积分中注意要对复杂的分式结构进行分离常数再积分,不然很难受

解
[!done]-
解 由于积分区域
记原积分为
下面我们用两种方法来计算
(法一) 在直角坐标系下计算
如图所示,区域
其中
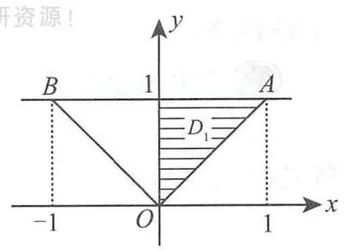
因此,
(法二) 在极坐标系下计算
在极坐标系下,
因此,
注 法二中最后一步计算用到了
如果对余切函数
Jun 19, 20254 min read
[!question]+
设
[!NOTE]+
二重积分中注意要对复杂的分式结构进行分离常数再积分,不然很难受

[!done]-
解 由于积分区域
记原积分为
下面我们用两种方法来计算
(法一) 在直角坐标系下计算
如图所示,区域
其中

因此,
(法二) 在极坐标系下计算
在极坐标系下,
因此,
注 法二中最后一步计算用到了
如果对余切函数