方向导数

方向导数研究的还是这个变化率的问题，以前传统的导数是大家默认的坐标轴方向，也就是沿着x轴和y轴这两个方向，方向导数定义了函数沿着任意方向的变化率，通过定义增量的微小的距离来衡量这个变化率

方向导数是一个数！

方向导数是一个数！是函数在 处沿着某个方向 上的变化率，这个方向通过 的方向余弦确定， 也是确定的，方向导数也就是确定的数
同样还要区分偏导数和偏导函数的概念，前者也是数，后者才是常常所求的所谓的偏导，偏导数一般是沿着坐标轴方向的方向导数
对于导数和导函数这俩概念也是同样的，导数是某点处的变化率的值，导数的连续的组合就是导函数，也就是对函数运用求导法则后的那些东西
这个方向导数应该对应是导数和偏导数这两个在某点变化率的数值概念，而梯度就是导函数和偏导函数这两个数值集合的函数概念，不过这里的梯度是一个向量，而不再是一个函数，导数可以理解为是一个映射

设三元函数 在点 的某空间邻域 内有定义, 为从点 出发的射线, 为 上且在 内的任一点,则

以 表示 与 之间的距离,如图 17-4 所示,若极限

存在,则称此极限为函数 在点 沿方向 的方向导数,记作 .

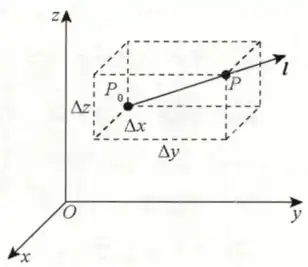
可以通过偏导数来简化这个用三个方向上的极限定义的过程，也就是方向导数的计算

个人理解部分，看可汗学院的视频得来的

我们是通过正交坐标轴来定义的这个方向上的微小的变化量 ，这个距离也就是在xy方向上的线性组合来的嘛

所以这个方向导数的方向也就是这个偏导数的某种线性组合