题20

[!question]+
(20) (本题满分 11 分)

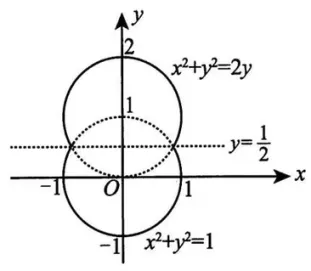
一容器的内侧是由图中曲线绕轴旋转一周而成的曲面,该曲线由与连接而成.
( I ) 求容器的容积;
( II ) 若将容器内盛满的水从容器顶部全部抽出, 至少需要做多少功?
(长度单位: ,重力加速度为 ,水的密度为 )

[!NOTE]+
这里应该怎么去套这个旋转体的体积公式，我的直觉犯了两个错误，第一个就是对这个x的意识不了解，第二就是忘记了这也是一个二重积分，可以自己调整积分区域，然后再去计算。

[!done]-

注意第二问这个划分区间到一起的这个技巧

(解) (I) 如图 (a) 所示,旋转体可看作由图中阴影区域绕轴旋转一周所得,由两部分组成, 是由区域绕轴旋转而成的旋转体的体积, 是由区域绕轴旋转而成的旋转体的体积.

由于曲线与曲线关于对称,故 . 旋转体的母线可取为 .

因此,该容器的容积为 .

(II) 用元素法,取图 (b) 中阴影部分的小薄片为做功的元素. 该小薄片近似于高为的圆柱体. 当时,小薄片的底面半径 ; 当时,小薄片的底面半径为 . 小薄片提升的高度近似为 ,克服该小薄片形状的水的重力所做功为

因此,

由于

故

因此,所求的功为 .

YiNotes