定积分的应用

平面图形的面积

00:43:30

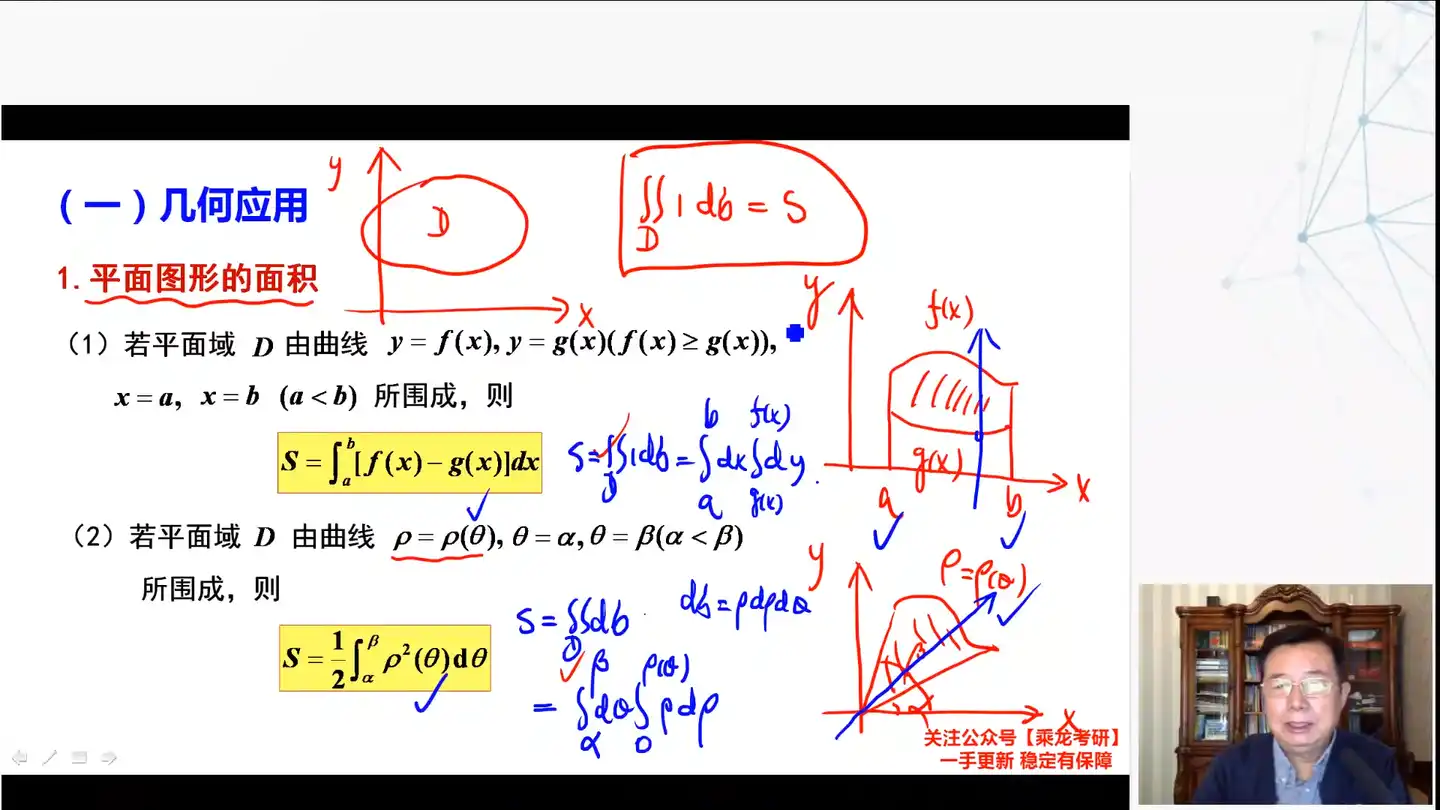
所有的面积问题都可以用一个公式概括，也就是这个二重积分的定义式

Q:平面由曲线 ， 所围成，面积怎么算？

A:函数上下之差就是夹起来的面积

极坐标表示区域面积

Q:平面由 所围成那么面积是多少？极坐标面积的算法和三角形很像

A:像是三角形的面积公式似的

Link to original

旋转体的体积

以例10.1为例，如果旋转的这个函数是对称的，只旋转一半，也就是积分的上界要注意只取一半

曲面绕y轴旋转一周的体积

曲面绕x轴旋转一周的体积

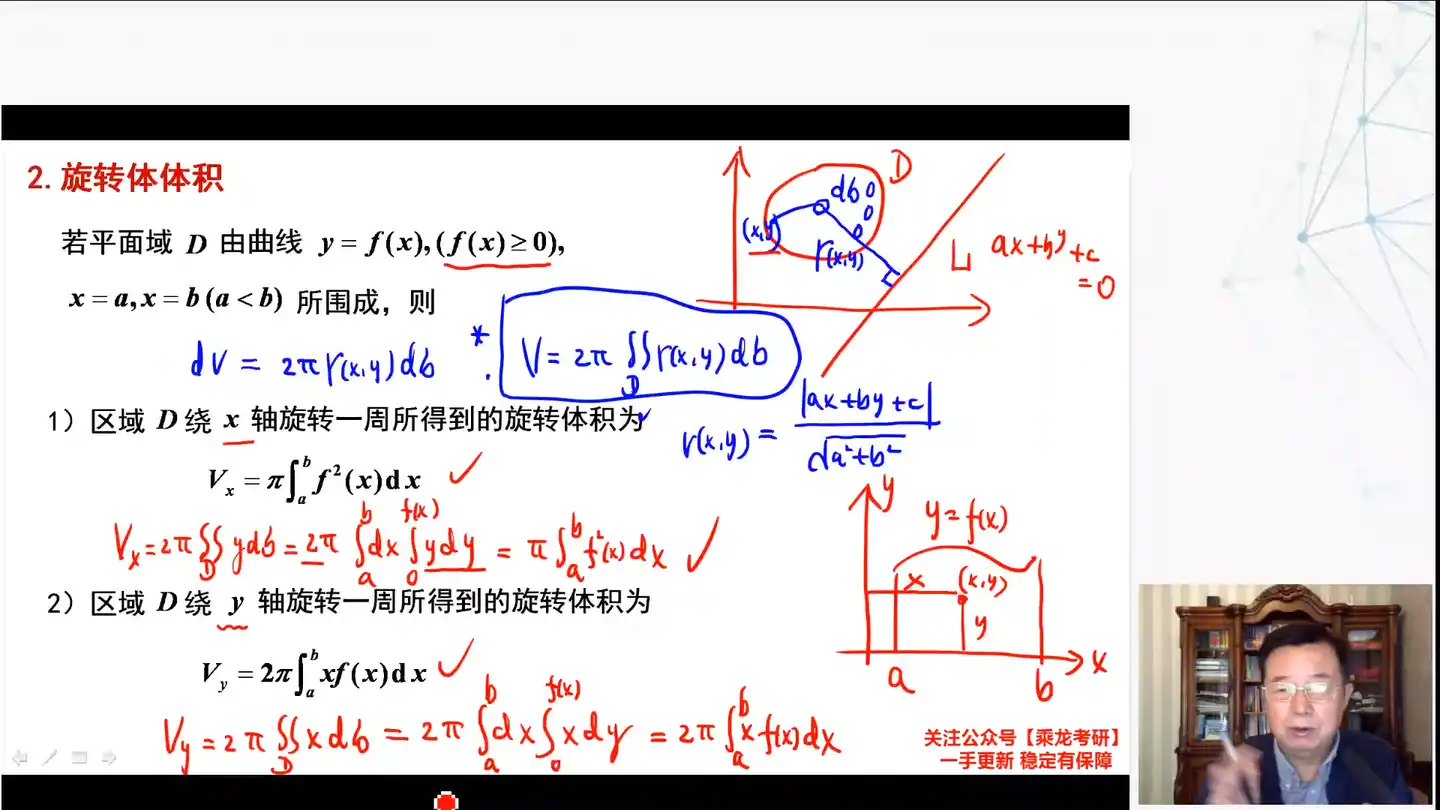
Q:旋转体的体积公式可以总结为这么一个公式, 也就是古尔丁定理

A: ，其中 为点到直线的距离
若平面域 由曲线 所围成, 则
微元 , * , 其中 为点到直线的距离

1. 区域 绕 轴旋转一周所得到的旋转体积为
   利用微元法，可以推导出该公式：
2. 区域 绕 轴旋转一周所得到的旋转体积为
   
   利用微元法，可以推导出该公式：

Q:极坐标下的古尔丁定理算旋转体体积？

A:以例10.1作为说明
绕着Ox轴，也就是绕极轴旋转一周的体积，对y二重积分
，极坐标换元中，，代入有
，转化为两次一重积分，得到
，其中是极坐标下的曲线方程

Link to original