特征值衡量的是变换中拉伸的程度,是通过变换中不变量,也就是特征向量的拉伸程度来衡量的,它是矩阵变化的程度的指标
这样的变换,显然就是所谓的存在维度上的降低,特征值对应的特征方程的矩阵的行列式显然就是0,也就是存在维度上的变化,因为有的向量没动
特征值的性质和结论
Q:如何判断
A:
常考这样一个行列式:【注】这里常见的命题方法: 若
Q:矩阵的行列式和矩阵的迹与特征值存在等价关系
A:也就是特征值之和是矩阵的迹
特征值之积是矩阵的行列式的值
同时
k阶主子示去掉同行同列后的行列式 12:19
Q:秩1矩阵的特征值有一些相关迹的结论
A:也就是秩1矩阵的迹之和如果为0,那么这个矩阵的n重特征值全为0。如果迹不为0,那么这个矩阵的n-1重特征值为0,第n个特征值为它的迹
若
Q:秩1矩阵矩阵的迹和矩阵的特征值的关系
A:当
这个结论可以用不同的方法证明(需要重点事握)
证:法(方程组法)
若
由于
设
上下三角矩阵的特征值就是对角线上的元素
常用矩阵的特征值与特征向量
Q:常用矩阵的特征值和特征向量的对应关系
A:特征值是矩阵变换的拉伸效果的度量,站在这个角度上去想,这个数值的变化应该和变换矩阵的作用是对应的
| 矩阵 | A | ||||||
|---|---|---|---|---|---|---|---|
| 特征值 | |||||||
| 对应的特征向量 |
18:34

不可逆矩阵手动制造出来可逆矩阵,构造
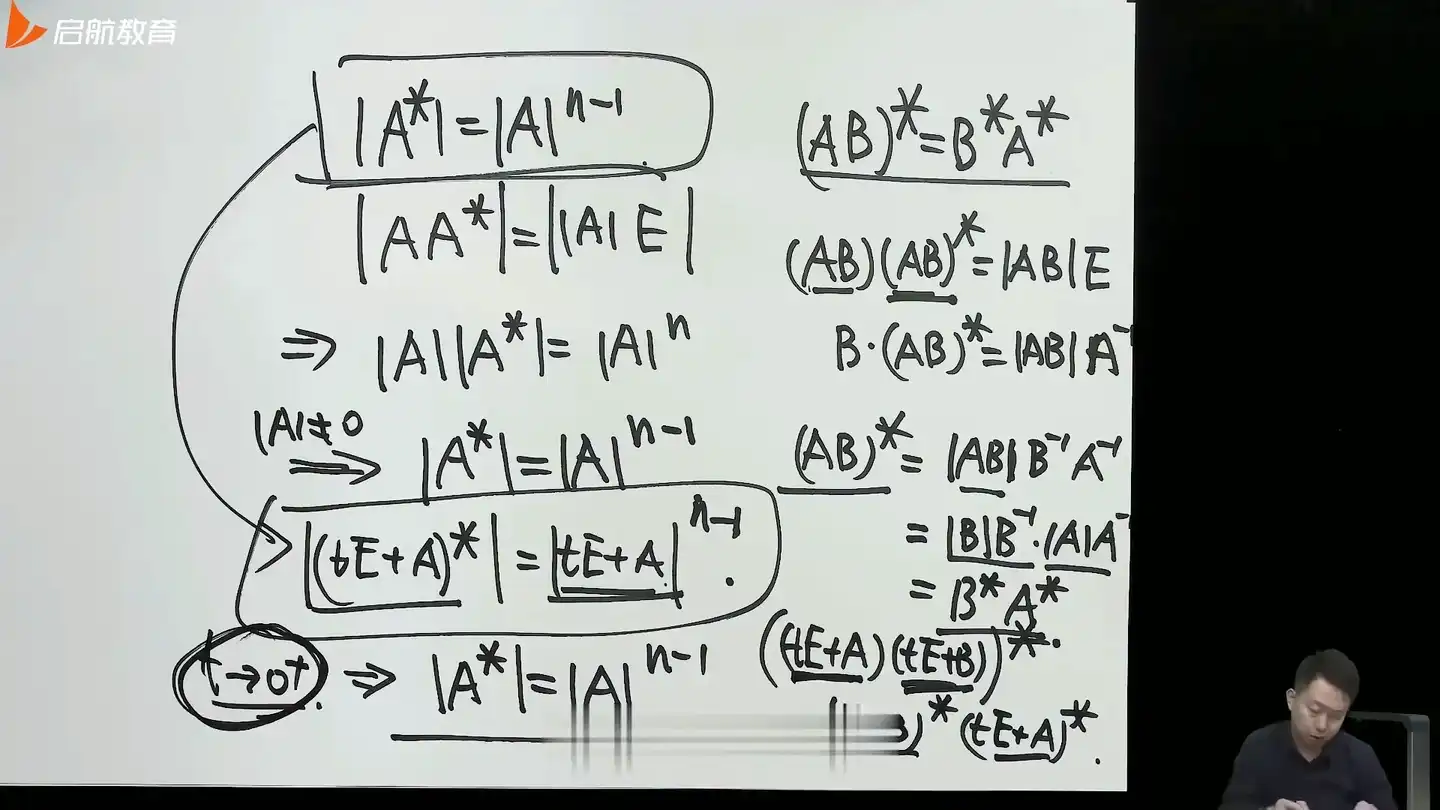
扰动法,这两个关于这个伴随矩阵的二级结论不可逆也是成立的
55:34

用不同的视角Q和R看同一个变化,在计算上的化简
正交矩阵
09:31

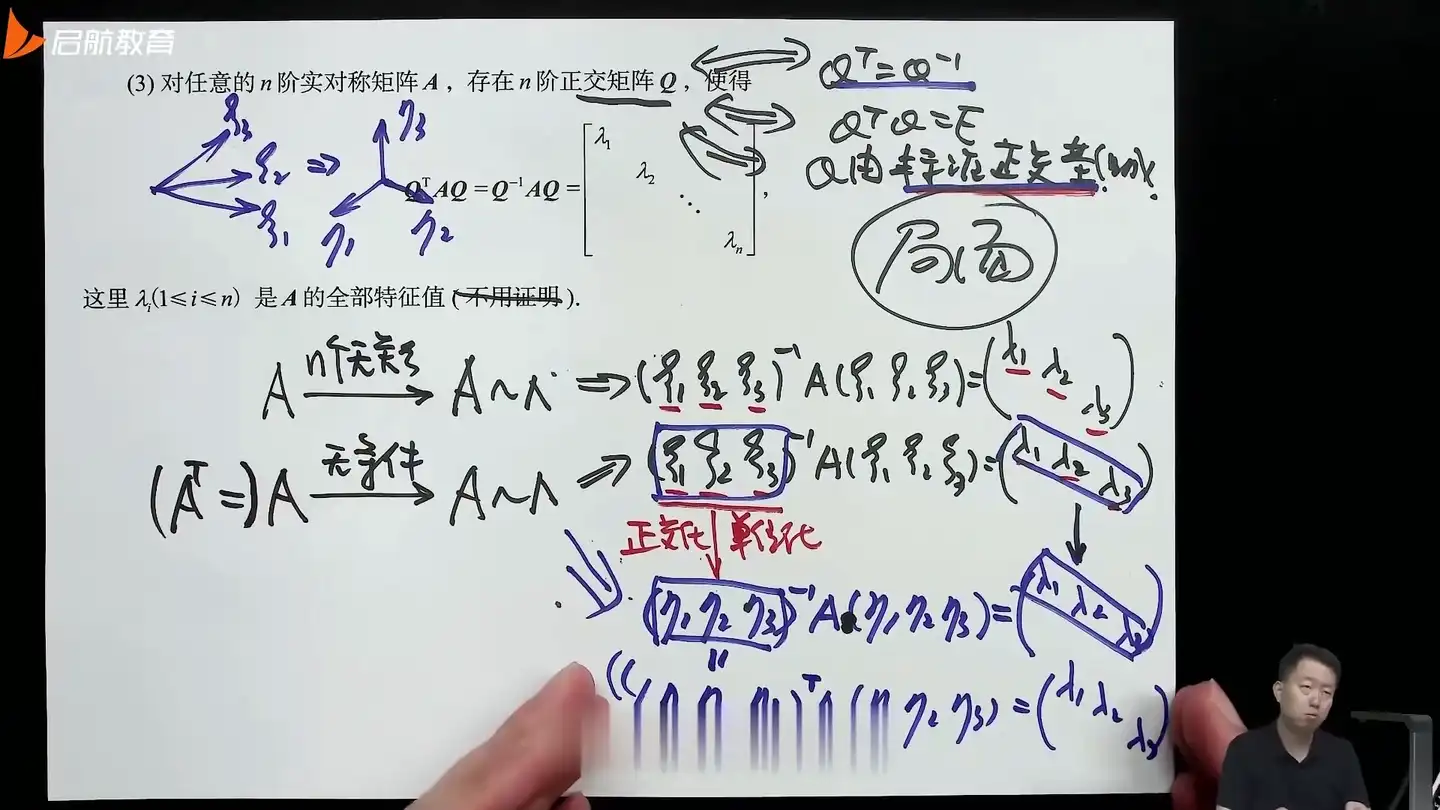
特征向量形成的P,肯定是能作为基的,但是为了性质更加漂亮,需要对这个基做正交化,变成这个基下的标准正交形态
上面这个操作是对实对称矩阵而言的
如果是一般的不具备对称性的矩阵,不能进行上面这个基正交化的操作
17:39
23:37

普通矩阵这里做正交化,会导致得到的正交的特征向量,无法对应回去原本的特征值
实对称矩阵一定可以通过正交化来达成相似对角化,但是普通的矩阵来做正交化以后,因为对应不回去原本特征值,是做不了相似对角化的,也就是,不能通过这个路径来做这个相似对角化
26:21

证明这个事情,用的是反证法
总的来说,一般的矩阵(前提是可以做相似对角化)那么就有相似对角化那个局面
对于更特殊的实对称矩阵,处理上面一般矩阵做相似对角化的办法,还能通过正交化的方式来做这个相似对角化
