矩阵乘法

你分析得很正确！矩阵乘法 可以看作是对矩阵 进行列变换，因此 的列向量可以用 的列向量线性表示。这意味着 的列空间是 的列空间的子空间，所以 总是成立的。

关于矩阵B是否满秩对结论的影响:

• 如果B满秩: 你的理解完全正确！当 满秩时，矩阵乘法 相当于对 的列向量进行线性无关的变换，不会丢失 列空间的维度信息。因此， 。
• 如果B不满秩:
  • 这时 的列向量组线性相关， 的列向量是 的列向量的线性组合，但这些组合系数可能存在冗余，导致 的列向量组线性相关性增加，列空间维度可能减小。
  • 但结论 仍然成立! 这是因为 的列向量仍然是 的列向量的线性组合， 的列空间仍然是 的列空间的子空间。将 和 放在一起并不会增加新的线性无关的列向量。

总结:

无论 是否满秩， 总是成立的。

如何理解B不满秩时，AB中B对A的作用:

可以将 不满秩时对 的作用理解为一种“信息压缩”或“降维”的操作。 将 的列向量映射到一个低维的列空间中。

举个例子：

假设 是一个 的矩阵， 是一个 的矩阵，且 。这意味着 将二维平面上的向量映射到一条直线上。

尽管 不满秩， 的列向量仍然可以通过 的列向量线性表示，只是这些线性组合的系数存在冗余。

线性代数入门, page 50

矩阵乘法是 矩阵和向量的乘积 运算的自然推广

两个矩阵 A,B 能够相乘，亦即乘积矩阵 AB 能够存在，必须要求 A 的列数与 B 的行数相同

乘积矩阵 AB 的第 k 列是 , 这说明，只有 B 的第 k 列 会影响 AB 的第 k 列，而 B 的其他列不会影响 AB 的第 k 列

线代入门这里有点抽象，直接用自己的记法

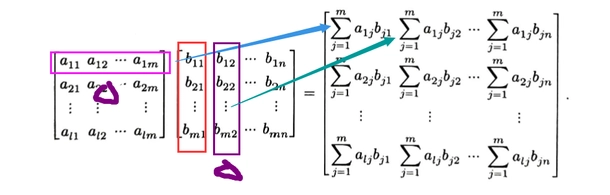
左侧取行和右侧的列向量做乘积运算，得到就是左侧行数为 i，后侧列数为 j 的元素的值，也就是，左侧第一行，右侧第二列，得到 c 的第一行第二列

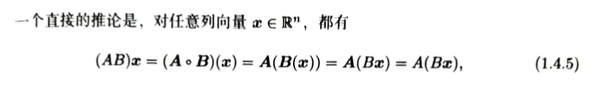
矩阵与列向量乘积和矩阵乘积有结合率
更一般的，乘法满足结合律

但是乘法的交换律和消去率不成立

两个非 0 矩阵的乘积可能是 0 矩阵

如果 AB 可交换， AB 一定是同阶方阵