题21
题目
[!question]+
已知函数 在 上具有 2 阶导数,且 . 证明:
(I) 存在 ,使得 ;
(II) 存在 ,使得 .
分析
[!NOTE]+

解
[!done]-
第 (I) 问,可以考虑构造辅助函数,找到两个不同的点,使得 在这两点的取值相同,再应用罗尔定理. 也可以考虑证明 在 上的最大值大于 1,从而由费马引理得到该点处的导数值为零.
费马引理 设函数 在点 的某邻域 内有定义,并且在 处可导. 若对任意的 ,都有 或 ,则 .
第 ( II ) 问,要证明存在 ,使得 ,可以考虑构造辅助函数 ,使得 ,再证明存在 ,使得 . 也可以考虑构造与 性质接近的函数 (满足 ),通过研究 来研究 .
(II) (I) (法一) 构造辅助函数 ,则 . 由拉格朗日中值定理可得,存在 ,使得 ,即 .
再对 上的 使用罗尔定理可得,存在 ,使得 .
(法二) 反证法.
由 在 上存在 2 阶导数可知 在 上连续. 若不存在 ,使得 ,则由 的连续性以及零点定理可知, 在 上恒大于零或恒小于零.
又因为 ,所以 恒大于零, 在 上单调增加. 是 在 上的最大值. 于是,
这与 矛盾.
因此,存在 ,使得 .
(法三) 证明 在 上的最大值大于 1 .
假设不然,则对于任意的 ,都有 ,从而 . 又因为 , 所以由 的连续性可知,存在 ,使得当 时, . 于是, .
这与 矛盾. 假设不正确.
因此, 在 上的最大值大于 1 . 如图 (a) 所示,记该点为 ,由于 , 故 .
由费马引理可知, .
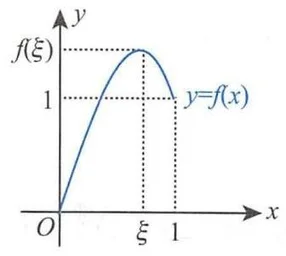
(a)
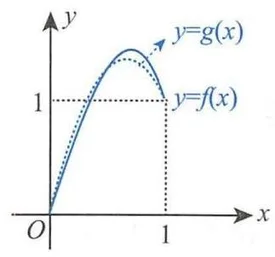
(b)
(II) (法一) 构造辅助函数 ,于是 在 上 2 阶可导,且
取 为第 问中满足 的点,则 .
由拉格朗日中值定理可得,存在 ,使得
存在 ,使得
再对 上的 使用拉格朗日中值定理,可得存在 ,使得
由于 ,故 ,从而 ,即 ,也即 .
(法二) 构造二次函数 ,使得 且
由 可得 . 由 可得 . 又由 可得 , 即 . 解得 . 于是,令 与 的图形如图(b) 所示.
考虑 ,则 ,且 .
下面我们证明,存在 ,使得 ,即 .
令 ,则 . 由拉格朗日中值定理可得,存在 , 使得 ,即 . 从而, .
分别对 上的 使用罗尔定理,可得存在 ,使得
再对 上的 使用罗尔定理,可得存在 ,使得 ,即 .
注 ① 下述命题为一加强版的积分中值定理.
若函数 在 上连续,则在开区间 内至少存在一点 ,使得
第 (I) 问中,也可以使用加强版积分中值定理以及 得到存在 , 使得 .
② 由 以及 可知,没有 满足 . 因此, 第 ( II ) 问的法二中,构造辅助函数 时,应考虑将 设为二次函数 .


