题18
题目
[!question]+
设函数
分析
[!NOTE]+

解
[!done]-
已知条件给了
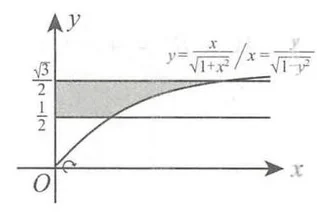
由本题图形的特点以及旋转轴为
若旋转体由区域
解
(1) 式中的
原方程乘以
(3) 式 - (2) 式消去
将
由
由旋转体的体积公式可得, 所求旋转体体积
Jun 19, 20253 min read
[!question]+
设函数
[!NOTE]+

[!done]-
已知条件给了
由本题图形的特点以及旋转轴为
若旋转体由区域
解
(1) 式中的
原方程乘以
(3) 式 - (2) 式消去
将
由
由旋转体的体积公式可得, 所求旋转体体积
