题3

题3

题目

设函数 在 处连续,则 ( )
(A) .
(B) .
(C) .
(D) .

分析

这里的核心是无穷小乘有界这种结构，特别是，这个和要怎么取，才可以让左边是无穷小，右边是有界，这个结构考了很多遍了
对于这种分段的函数求导，或者求极限，判断是否存在间断点的，我经常有疑问什么时候用公式，什么时候直接用定义，我们在真题：题3中同样有这个问题，这种题目还可以结合变限积分来考。

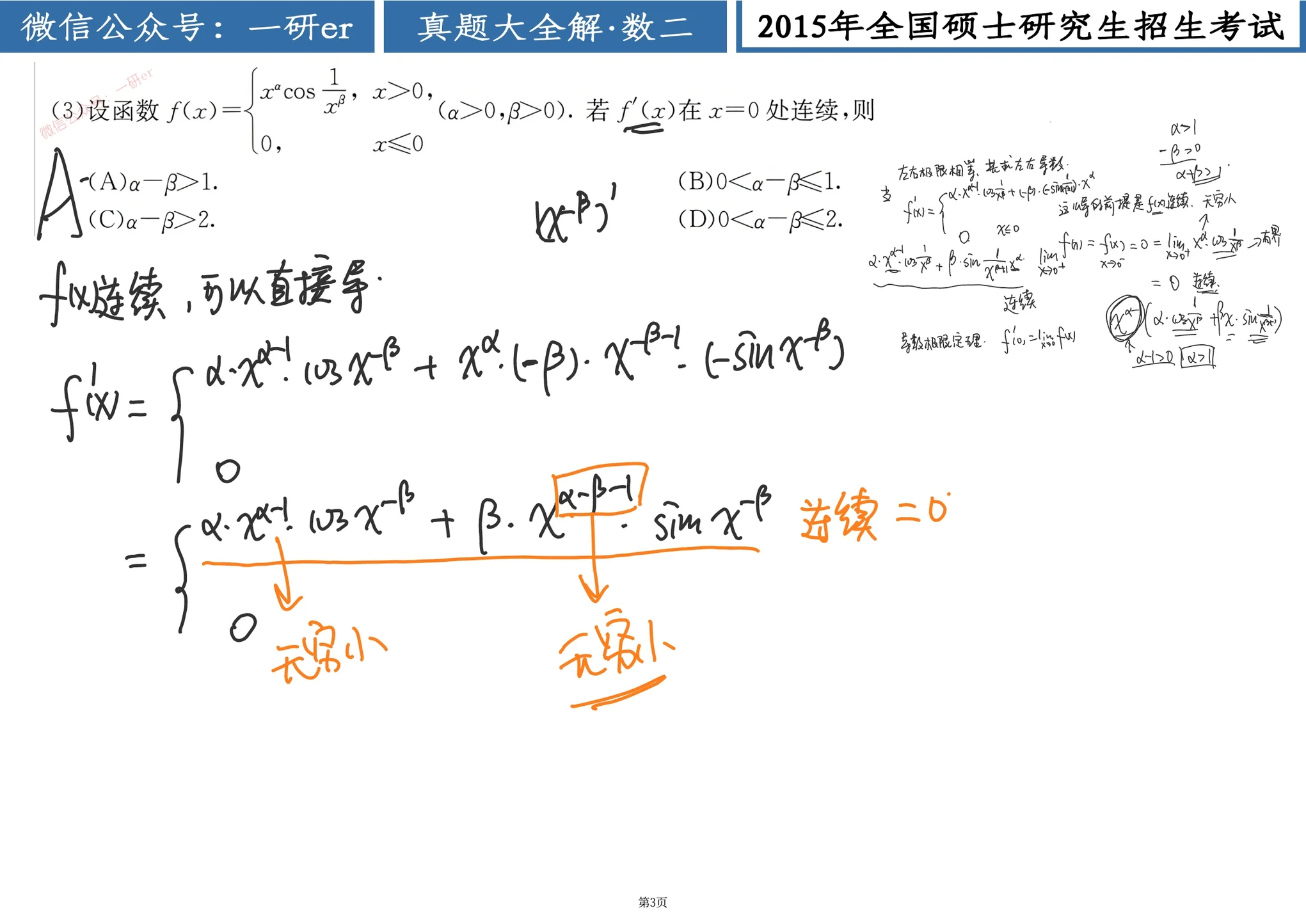
解

解 首先求 .

根据导数的定义,

由于 在 处连续,故 存在,从而

由于当 时, 有界但 不存在,故 当且仅当 .

由上可知,当 时, .

还需要再检查 成立的条件.

当 时, ,故当 时, ,从而 .

当 时,

由于 ,故

由于当 时, 有界但 不存在,故 当且仅当 , 即 .

联立 可得 . 应选 A.

注 解本题要求对导数的概念有正确把握. 函数在某点处的导数存在指的是该点处的左侧导数和右侧导数均存在且相等, 而导函数在某点处连续指的是导函数在该点处的左、 右极限存在且相等, 并且等于该点处的导数值. 这两个概念应区别开来. 有时候, 函数在某点处的导数存在,但它的导函数在该点处却并不连续. 例如