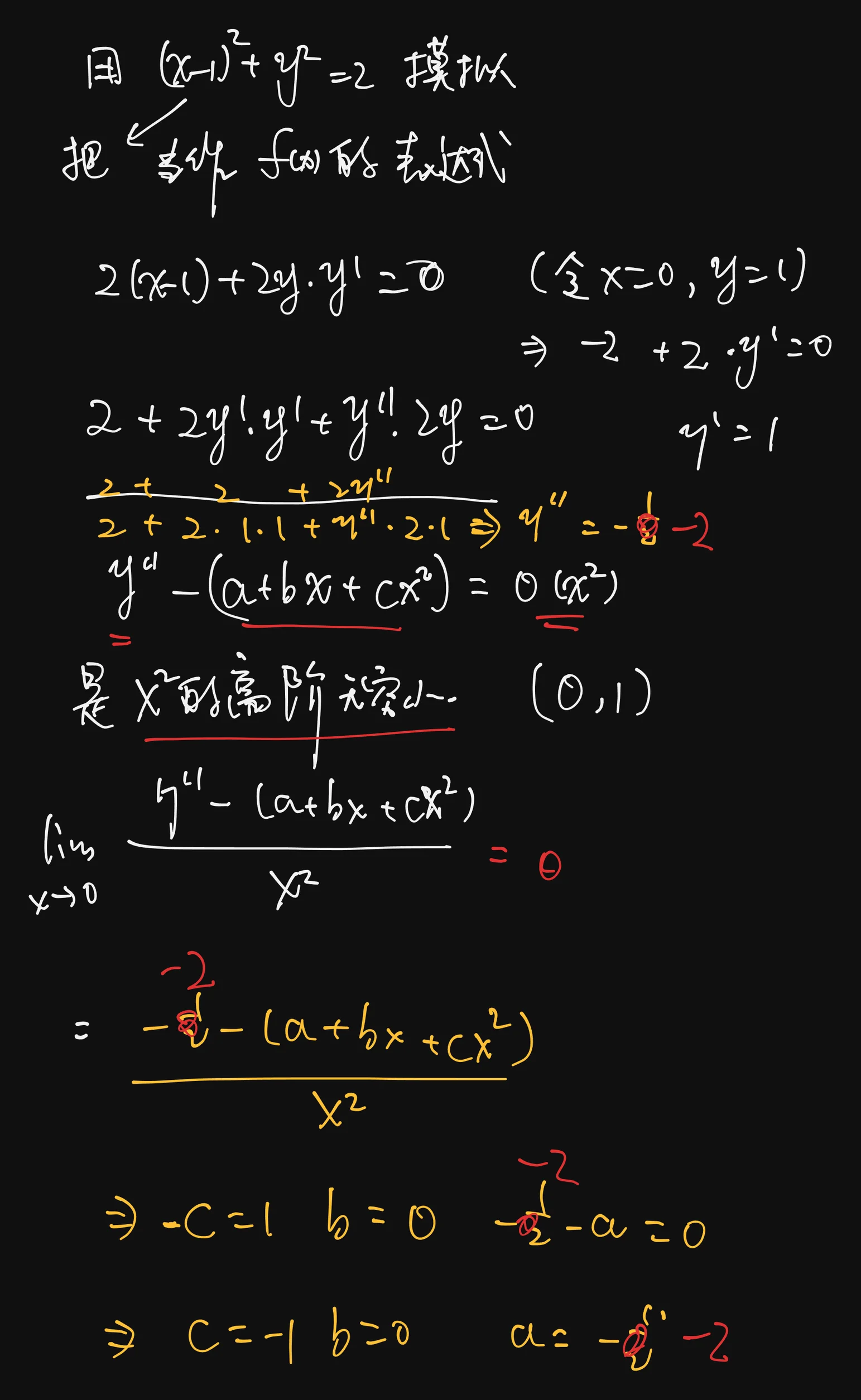例5.5

例5.5

题目

Q:P118 (仅数学一、数学二) 已知曲线 在点 处的曲率圆方程为 , 且当 时,二阶可导函数 与 的差为 ,则 ( ).
(A)
(B)
(C)
(D)

分析

A:很多年真题考过，邂逅遗憾说是重点
葫芦直接看出来是皮亚诺型余项泰勒公式，因为给了点，还给了关于的无穷小余项，所以应该是泰勒来对比系数
关键在于直接把曲率圆方程视作是f(x)的最佳近似，然后因为曲率圆和该f(x)在同一处有相同的切线，又可以对x求偏导数，构造微分方程的形式，来进一步得到f(x)导数的值和性质

解

应选(C).
由题意可知,点 在曲线上,故 .
对曲率圆方程 关于 求导,得

故可得

即有 .
对 式两边关于 求导,得

代入 ,可得 .
故当 时,有

故由题意知, .