题5
题目
[!question]+
(5) 若 不变号,且曲线 在点 处的曲率圆为 ,则函数 在区间 内 ( )
(A) 有极值点, 无零点.
(B) 无极值点, 有零点.
(C) 有极值点, 有零点.
(D) 无极值点, 无零点.
分析
[!NOTE]+
不太懂曲率圆这个条件有什么用,在例5.5里面直接把它当做是的表达式,也就是解答里面的法二
我觉得有极值点但是没有零点
解
[!done]-
应该选B,无极值点,有零点
这里要明确的是:曲线 在某点的曲率圆与曲线在该点具有相同的切线和曲率,且在该点附近具有相同的凹凸性. 在实际问题中,常用曲率圆在点 附近的一段圆弧来近似代替曲线弧,使问题简化.
我下面的问题是,可以直接拿圆的凹凸性质当做f(x)的,就可以确定二阶导的正负
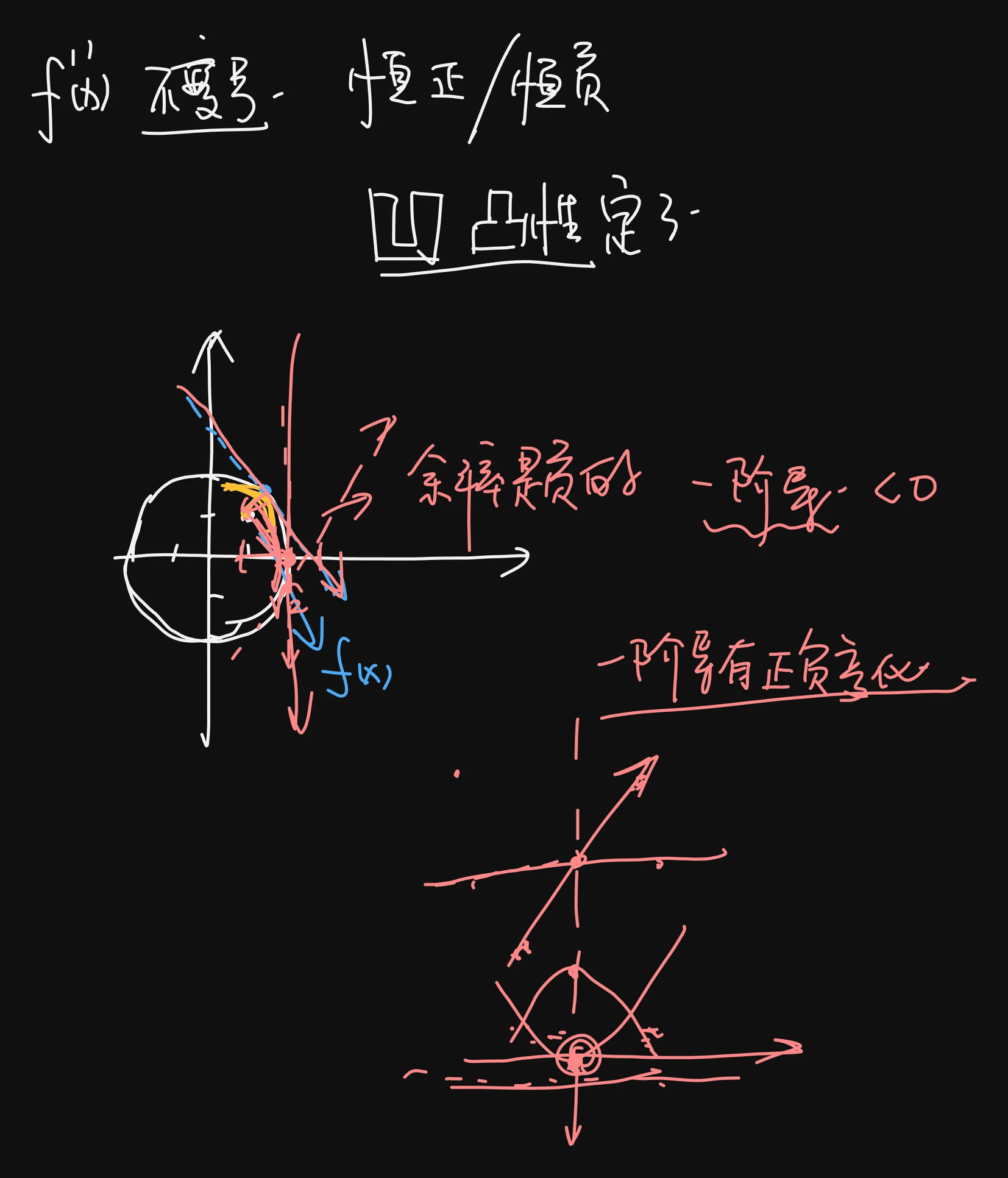
解 (法一) 由于曲线 在点 附近的凹凸性与点 处的曲率圆的凹凸性一致,而曲率圆为 ,是凸曲线,故 .
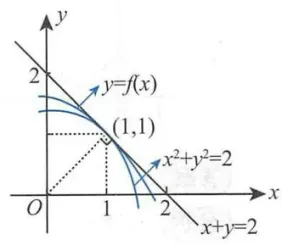
考虑曲线在点 处的切线.
连接点 和点 的半径为点 处的法线,该法线斜率为 ,于是点 处的切线斜率为 -1,即 .
由于 不变号,故在区间 上,仍有 ,从而 在 上单调减少. 又因为 ,所以 在 上恒小于零. 于是 在 上单调减少. 因此, 在 上没有极值点.
再考虑 在 上的零点情况.
由拉格朗日中值定理知,存在 ,使得 ,即 .
由于 在 上单调减少,且 ,从而 ,故 .
因为 ,所以由连续函数的介值定理知, 在 上存在零点.
因此, 在 上有零点,没有极值点. 应选 B.
(法二) 由于曲线 在点 附近的方程可由它在点 处的曲率圆方程来近似, 即 ,故我们可以用该方程算出 和 .
对 两端关于 求导,得
代入 得, . 继续对 (1) 式两端求导,得
代入 得, .
由于 不变号,故 在 上恒小于零.
其余论证 在 上有零点,没有极值点的过程同法一.
注 在法一中,我们并没有求 的值. 不过我们也可以利用曲率与曲率半径的关系,结合曲率计算公式 求出 . 代入 (这是因为曲率半径为 ,可计算得 . 再由 可知 .

