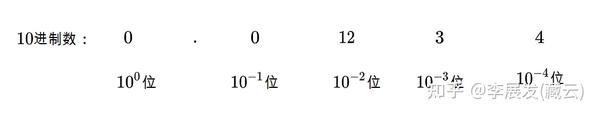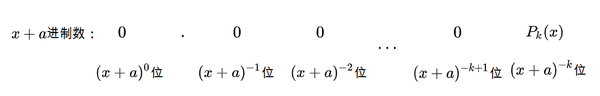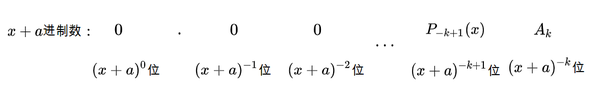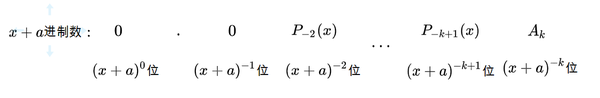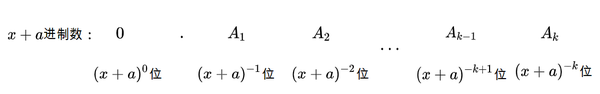第三步:分解真分式
我们设
因此我们可以把真分式分解为四种基本类型的部分分式:
对于第3、4种部分分式,我们注有“
接下来,我们证明以上四种分式,特别是第2、4种分式,可以再进一步分解为更简单的、可积分的分式之和。
第一种分式
第一种分式
首先,对于分母为
的式子: 显然,
应是一个常数,因为如果它包含有一个 ,那么这个式子就不是个真分式(其实不会出现这种情况),就可以用分式除法继续化简为 的形式: Link to original
第二种分式
第二种分式
对于分母为
的式子: 同样,分子应当是一个常数。因为如果分子包含有
,就必定存在一个假分式因子,该假分式因子可以通过除式除法进一步化简: 现在,我们说一个真分式:
它可以进一步化简为以下几个分式之和:
因为它是一个真分式,所以
中的 的最高次幂必然是小于 的。我们上面已经讲了如果 的形式。我们来看 时: 无论
是多少次幂(小于 k)的多项式,都可以通过这种方式计算,从而分解为:
我们也可以使用“进制”的思想来理解这一点。不感兴趣的可以不看。
首先,一个有理真分数大于0小于1,即:
, , 为整数。它可以表示成一个小数。例如 。我们的问题就变成怎么把它表示成 :
先拿
,变成:
,变成:
,变成:
因为这个真分数小于1,因此必然
位之前停下来。 我们把这个步骤重复在
中,我们可以把它看成 ,即它是 (x+a)进制的,小数点后 位上的数是 :
我们使
,变成:
重复这个过程,如果
位上,值为 :
这个过程最多可以再进行一步,并停止在
位置上。计算 :
表示为十进制即:
Link to original
第三种分式
第三种分式
对于分母是
的式子: 显然
应该是一个一次多项式或常数,即 ( 可以为0,此时是一个常数)。 因为如果
中包含 或更高次幂的 ,那么它就不是一个真分式(其实不会出现这种情况),因此可以通过分式除法,对其进一步化简为 ,例如: Link to original
第四种分式
第四种分式
第四种分式:
同理,
应该一个一次多项式或常数,即 ( 可以为0,此时为常数的情况)。 因为如果
中包含 或更高次幂的 ,那么必然有个假分式因子,该假分式因子可以通过分式除法进一步化简: 接下来的叙述跟第二种分式中的是一样的,我们说一个真分式:
可以分解为以下分式之和:
它的证明跟第二种分式中的是一样的。我们这里不再赘述,两者的不同之处在于,在第二种分式中,
,根据分式除法,它的余式是一个常数,所以第二种分式分解后的所有分式分子是一个常数。但是在这里第四种分式中,因为分母是一个二次多项式 ,根据分式除法, ,它的余式是 ,这就是为什么这里所有分式分子形如 。
使用“进制”的思想,理解这一点,跟第二种分式中叙述的是一样的。不再赘述。
Link to original
分解出来的四种部分分式
到这里,我们可以确定,一个真分式可以化简为以下四种部分分式之和:
第一种分式
第二种分式
第三种分式
第四种分式Link to original
最终分解规则
分解出来的四种部分分式
到这里,我们可以确定,一个真分式可以化简为以下四种部分分式之和:
第一种分式
第二种分式
第三种分式
第四种分式Link to original 经过上面的讨论,我们可以知道,一个真分式经过因式分解之后:
一,如果包含有
这种因式,那么分解后有一个 的部分分式 二,如果包含有
这种因式,那么分解后有 三,如果包含有
这种因式,那么分解后有一个 的部分分式 四,如果包含有
这种因式,那么分解后有有一个 例如:
Link to original