题20
题目
[!question]+
已知曲线
分析
[!NOTE]+

应用题的核心就是链式法则
解
[!done]-
本题中,
本题中,既可以利用定积分计算
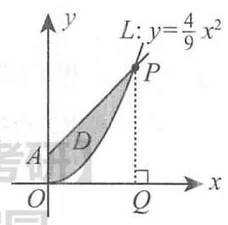
解 曲线
下面用三种方法计算
(法一) 区域
由图可知,梯形
根据定积分的几何意义,曲边三角形
因此,
(法二) 直线
根据定积分的几何意义,
(法三) 由法二可得直线
将区域
根据二重积分的几何意义,
根据链式法则,
当
因此,所求
Jun 19, 20254 min read
[!question]+
已知曲线
[!NOTE]+

应用题的核心就是链式法则
[!done]-
本题中,
本题中,既可以利用定积分计算

解 曲线
下面用三种方法计算
(法一) 区域
由图可知,梯形
根据定积分的几何意义,曲边三角形
因此,
(法二) 直线
根据定积分的几何意义,
(法三) 由法二可得直线
将区域
根据二重积分的几何意义,
根据链式法则,
当
因此,所求