题3
题目
已知数列 满足 ,则当 时, ( )
(A) 是 的高阶无穷小.
(B) 是 的高阶无穷小.
(C) 是 的等价无穷小.
(D) 是 的同阶但非等价无穷小.
分析
不要怀疑自己,直接宏观上考虑趋势就可以了,本质上这个题目考察的是数列里面带着三角函数的几何放缩+压缩映射,这个题目我们再张宇的强化里面做过,只不过是以大题的形式出现的:例2.20
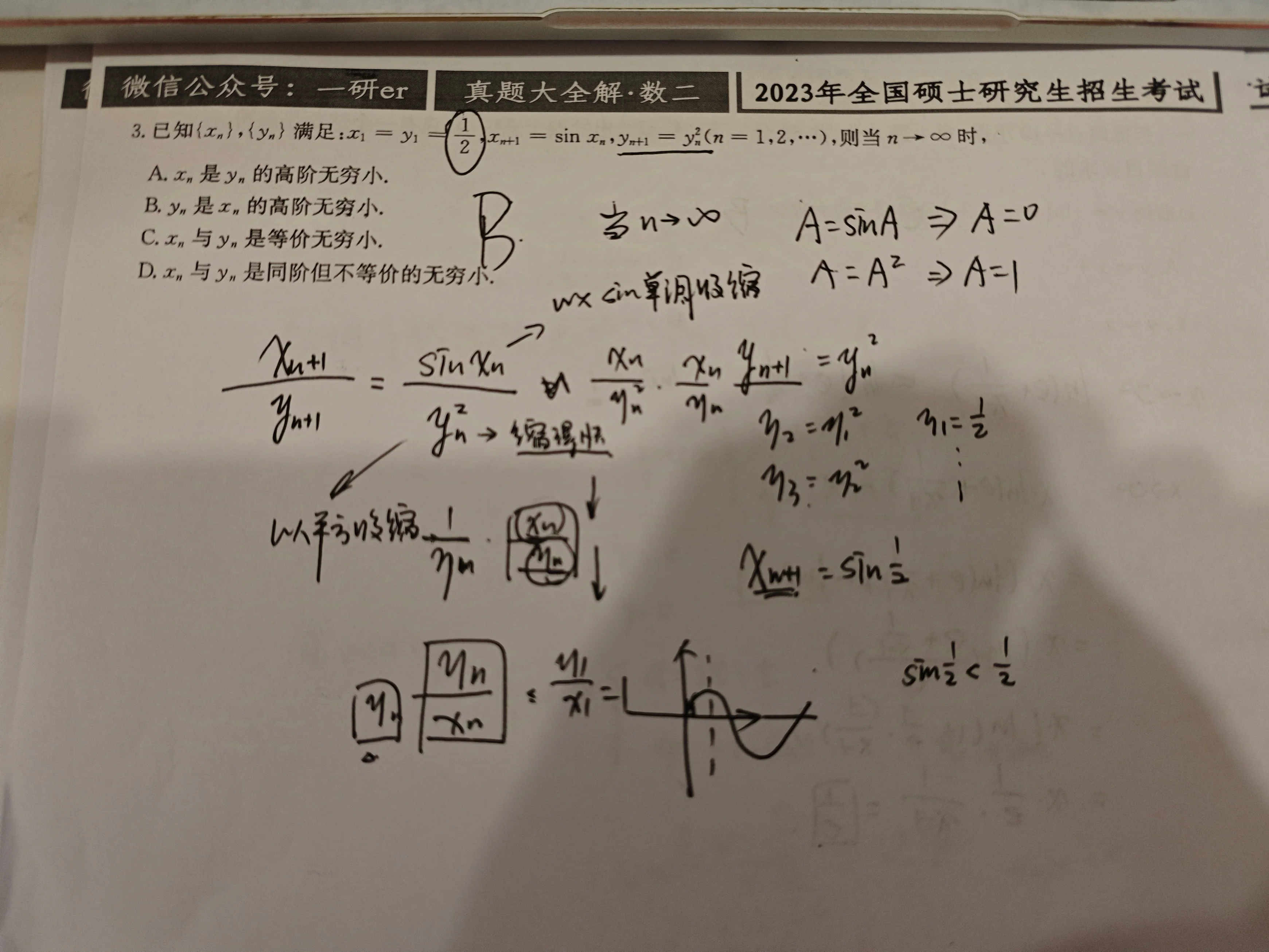
解
解 (法一) 首先证明对任意正整数 .
当 时, .
假设 ,则 . 由数学归纳法可知对任意正整数 .
由 的泰勒公式可知,存在 ,使得
于是,
由 可知 .
因此,
由于 ,故由夹逼准则可知, .
综上所述,当 时, 是 的高阶无穷小,应选 B.
(法二) 首先我们证明,在 内, ,即 .
令 ,则 . 注意到 的分母恒大于 0,故考虑分子的符号.
令 ,则 . 于是, 在 内单调减少. 结合 ,可得 ,从而 在 内小于 0, 在 内单调减少. 因此,当 时, ,即 .
由法一可知,对任意正整数 ,从而由前面的分析可得
下面我们证明,对任意正整数 ,从而 .
当 时, .
假设 ,则 . 由数学归纳法可知对任意正整数 , 从而 .
因此,
由于 ,故由夹逼准则可知, .
综上所述,当 时, 是 的高阶无穷小,应选 B.
注 下面证明 是 时的无穷小.
由法一可知, ,于是 单调减少. 结合法一中所得结论 “对任意正整数 ” 可得, 单调有界,从而 存在,记为 . 对 两端取极限可得, ,即 ,解得 .
此外, 也是 时的无穷小.
