题7
题目
[!question]+
(7) 设
(A)
(B)
(C)
(D)
分析
[!NOTE]+
这里看错题目了,要选错误的是什么
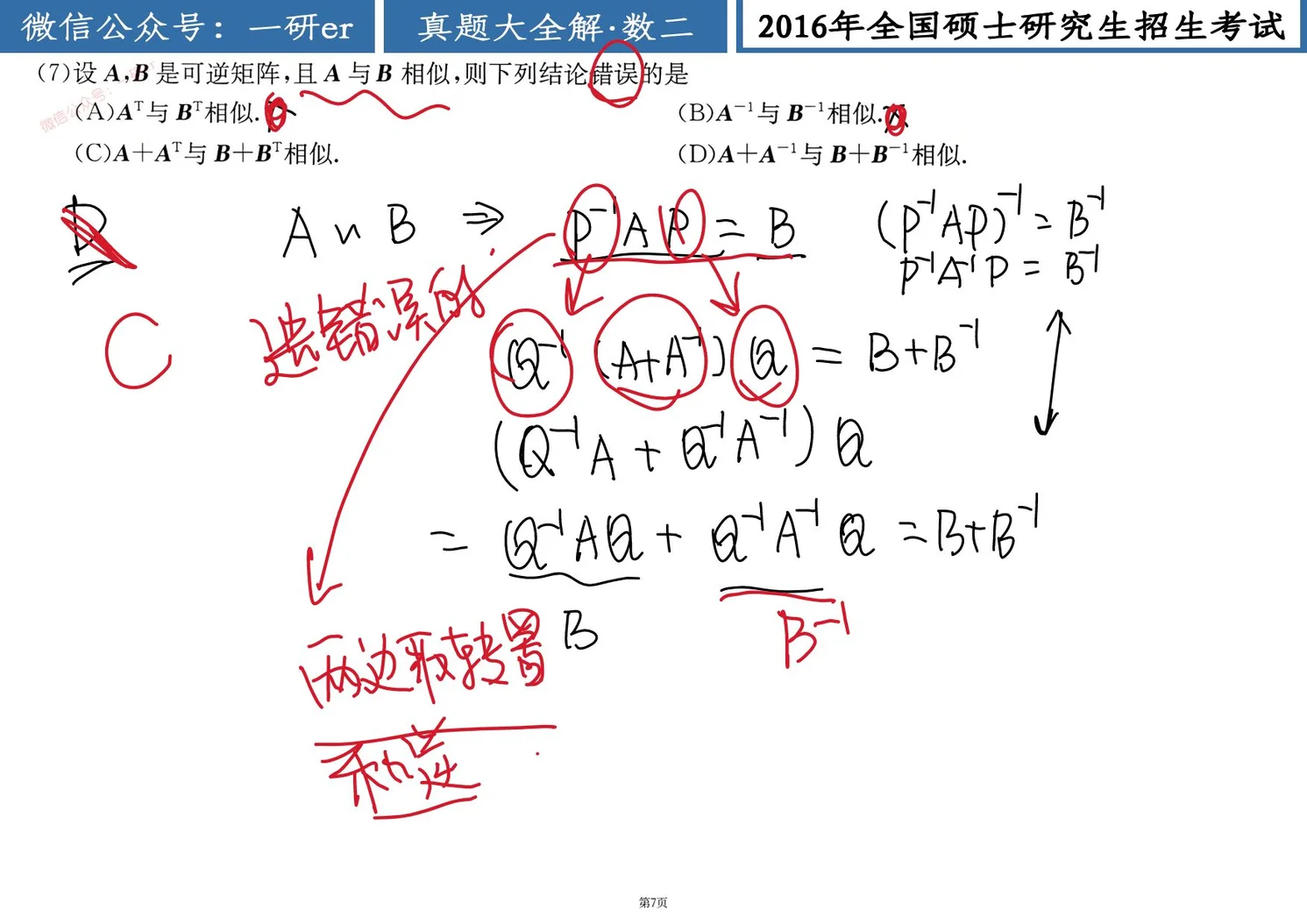
解
[!done]-
从选项
此外, 请注意矩阵乘积的转置和逆的计算.
若
若
解 由于
,选项 中的结论正确. ,选项 中的结论正确. - 由
和 可知, ,选项 D 中的结论正确. 由排除法可知,应选 C.
下面我们举例说明选项
设
则
计算
注
下面简单证明一下该结论.
若
Jun 19, 20253 min read
[!question]+
(7) 设
(A)
(B)
(C)
(D)
[!NOTE]+
这里看错题目了,要选错误的是什么

[!done]-
从选项
此外, 请注意矩阵乘积的转置和逆的计算.
若
若
解 由于
下面我们举例说明选项
设
则
计算
注
下面简单证明一下该结论.
若