题5
题目
设函数
(A) 1 .
(B)
(C)
(D)
分析
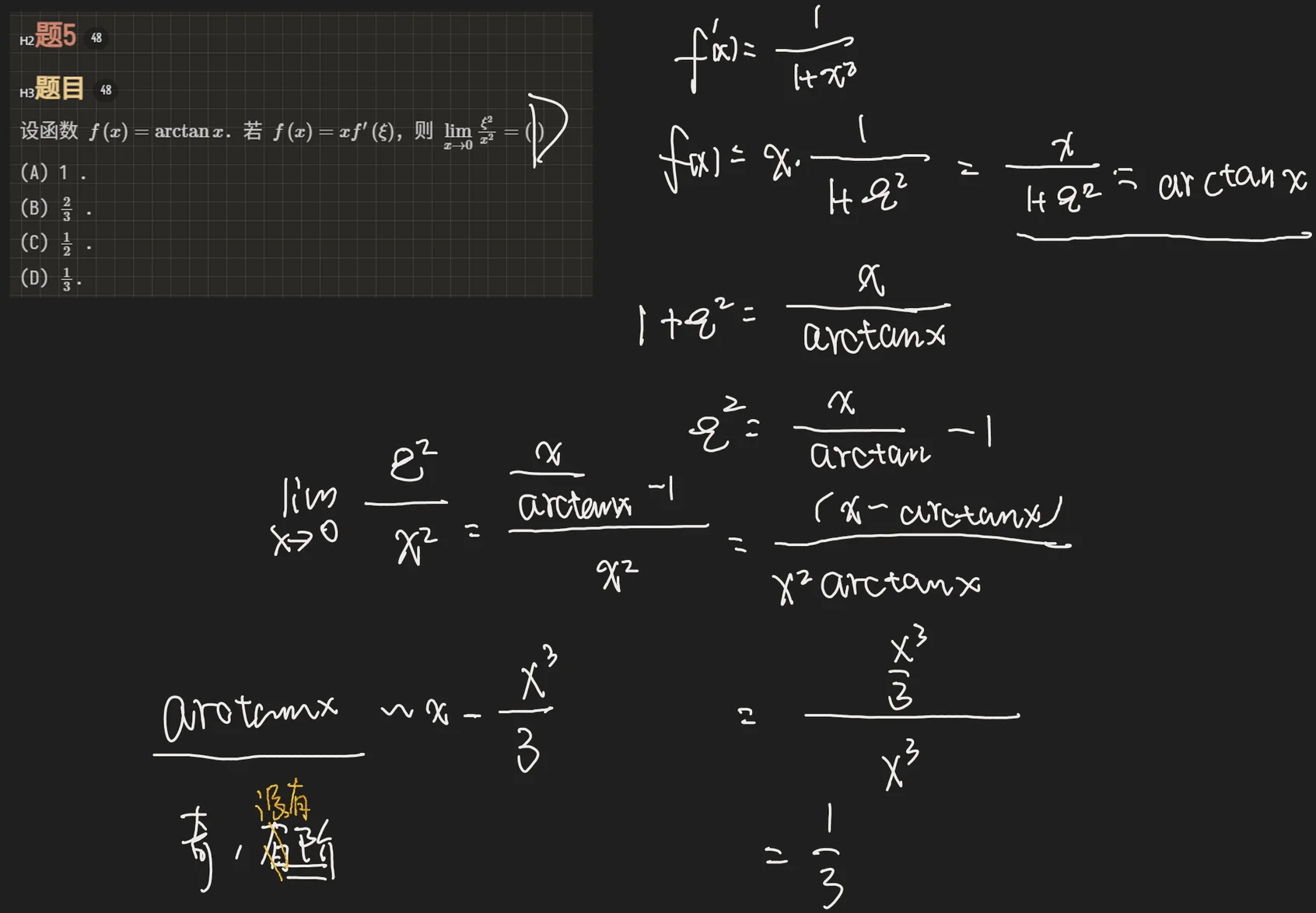
解
分析 本题主要考查未定式极限的计算. 本题的解题关键在于由已知条件写出
解 由于
得
下面我们用两种方法计算上面的极限.
(法一) 由于
应选 D.
(法二) 利用洛必达法则计算该极限.
注 ① 实际上,条件 “
对函数
由于
② 在计算中,要注意使用等价无穷小替换 “
Jun 19, 20253 min read
设函数
(A) 1 .
(B)
(C)
(D)
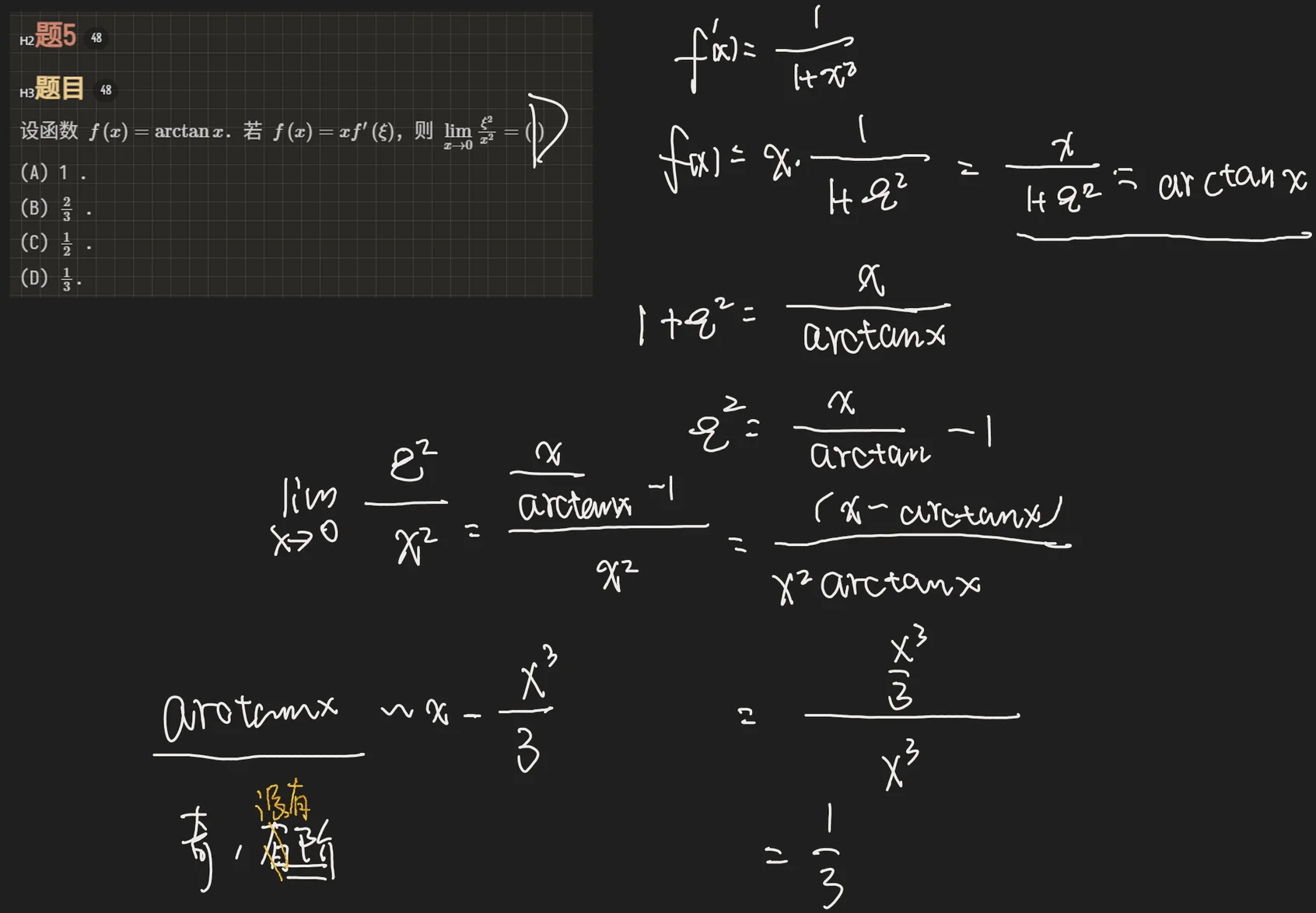
分析 本题主要考查未定式极限的计算. 本题的解题关键在于由已知条件写出
解 由于
得
下面我们用两种方法计算上面的极限.
(法一) 由于
应选 D.
(法二) 利用洛必达法则计算该极限.
注 ① 实际上,条件 “
对函数
由于
② 在计算中,要注意使用等价无穷小替换 “