(1)
【注 1 】这个方法主要适用于求
【注 2】积分后会“简单” 些的函数宜取作
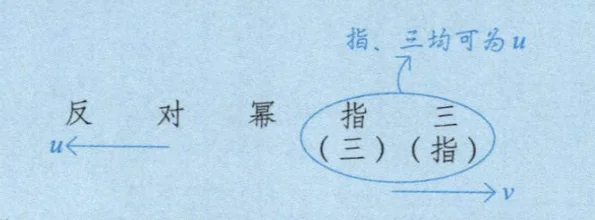
相对位置在左边的宜选作
(1) 被积函数为
(2) 被积函数为
(3) 被积函数为
(2) 分部积分法的推广公式与
设函数
则有
【注】证明
证明
联立以上式子, 得
事实上, 可写成如下表格

计算方法: 以
| 6 | 0 | |||
|---|---|---|---|---|
利用上述表格, 可得
原式
Jun 19, 20253 min read
(1)
【注 1 】这个方法主要适用于求
【注 2】积分后会“简单” 些的函数宜取作

相对位置在左边的宜选作
(1) 被积函数为
(2) 被积函数为
(3) 被积函数为
(2) 分部积分法的推广公式与
设函数
则有
【注】证明
证明
联立以上式子, 得
事实上, 可写成如下表格

计算方法: 以
| 6 | 0 | |||
|---|---|---|---|---|
利用上述表格, 可得
原式