题6
题目
[!question]+
设
(A)
分析
[!NOTE]+
轮换对称性简化二重积分,轮换x和y的位置,二重积分不变

解
[!done]-
若被积函数在积分区域上连续非负且不恒等于零, 则相应的二重积分大于零.
(解) (法一) 由于在第一象限内
(法二) 在极坐标系下计算
分别求得
(注) 利用轮换对称性,我们可以较快得出
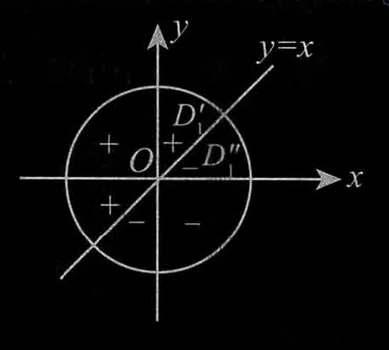
由此可以看出,
同理,
Jun 19, 20253 min read
[!question]+
设
(A)
[!NOTE]+
轮换对称性简化二重积分,轮换x和y的位置,二重积分不变

[!done]-
若被积函数在积分区域上连续非负且不恒等于零, 则相应的二重积分大于零.
(解) (法一) 由于在第一象限内
(法二) 在极坐标系下计算
分别求得
(注) 利用轮换对称性,我们可以较快得出

由此可以看出,
同理,