题19
题目
[!question]+
设函数
(I) 方程
(II) 方程
分析
[!NOTE]+

解
[!done]-
罗尔定理 若函数
第(I) 问要证明方程
通过观察发现,
此时,第 (I) 问的结论给出了
(II) 由于
从而
又因为
(II) 考虑
第 ( II ) 问等价于证明
若能找到三个点
由
由第 (I) 问的结论知,存在
另一方面,由于
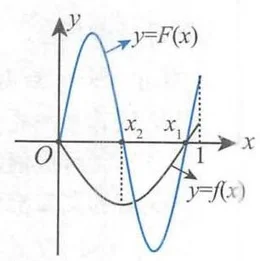
如图所示,
注 本题的证明思路: 找到三个点,使得函数
Jun 19, 20255 min read
[!question]+
设函数
(I) 方程
(II) 方程
[!NOTE]+

[!done]-
罗尔定理 若函数
第(I) 问要证明方程
通过观察发现,
此时,第 (I) 问的结论给出了
(II) 由于
从而
又因为
(II) 考虑
第 ( II ) 问等价于证明
若能找到三个点
由

由第 (I) 问的结论知,存在
另一方面,由于
如图所示,
注 本题的证明思路: 找到三个点,使得函数