题3

[!error]+
设函数在处具有 2 阶导数,则 ( )
(A) 当在的某邻域内单调增加时, .
(B) 当时, 在的某邻域内单调增加.
(C) 当在的某邻域内是凹函数时, .
(D) 当时, 在的某邻域内是凹函数.

[!note]+
例5.9没做对，这次也没有做对，我们再回顾一下导数极限定理和振荡间断点的定义，我觉得下面这个图我已经写得很清楚了：

[!done]-
函数的单调性与一阶导数的关系设函数在上连续,在内可导. 若在内 ,且等号只在有限个点处成立,则在上单调增加. (单调减少的情况对应于的情况. )

函数的凹凸性与二阶导数的关系设函数在上连续,在内二阶可导. 若在内 ,且等号只在有限个点处成立,则为上的凹函数. (凸函数的情况对应于的情况. )

在不确定一阶导函数的连续性的情况下, 单点处的一阶导符号不能确定该点邻域内的函数的单调性. 在不确定二阶导函数的连续性的情况下, 单点处的二阶导符号不能确定该点邻域内的曲线的凹凸性.

解注意到题目条件给出在处有二阶导数,故在处连续. 从而, . 结合极限的定义可得,存在 ,当时, . 于是, 在内单调增加. 应选 B.

下面说明选项 $、、$ 不正确.

当在的某邻域内单调增加时,我们能得到在该邻域内 ,但却不能保证 ,因为可能存在有限个点,在这些点处, . 例如 ,该函数在上单调增加,但是 . 选项不正确.

对选项 ,考虑 ,则为上的凹函数,但是 . 选项不正确.

对选项 D,我们可以考虑二阶导函数存在间断点的例子. 若为的间断点,则不成立,从而无法通过极限的定义得到的一个小邻域,在该小邻域内 .

考虑函数该函数在处存在二阶导数,但是在处不连续.

当时, . 当时,由导数定义,

因此,

在处连续.

当时,由导数定义,

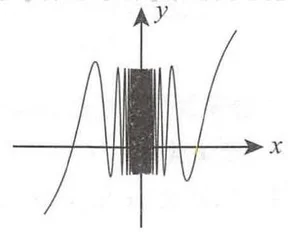
当时, . 如图所示, 在附近振荡, 振幅为 1,在附近不存在小邻域使得在该邻域上保持不变号,即不存在的小邻域, 使得在该邻域上是凹函数或凸函数. 选项 D 不正确.

YiNotes