题16
题目
[!error]+
设向量
分析
[!NOTE]+
矩阵里面两行两列两两不成比例,那么秩至少是2,这是因为这两个不成比例的行列,可以组成一个二阶主子式
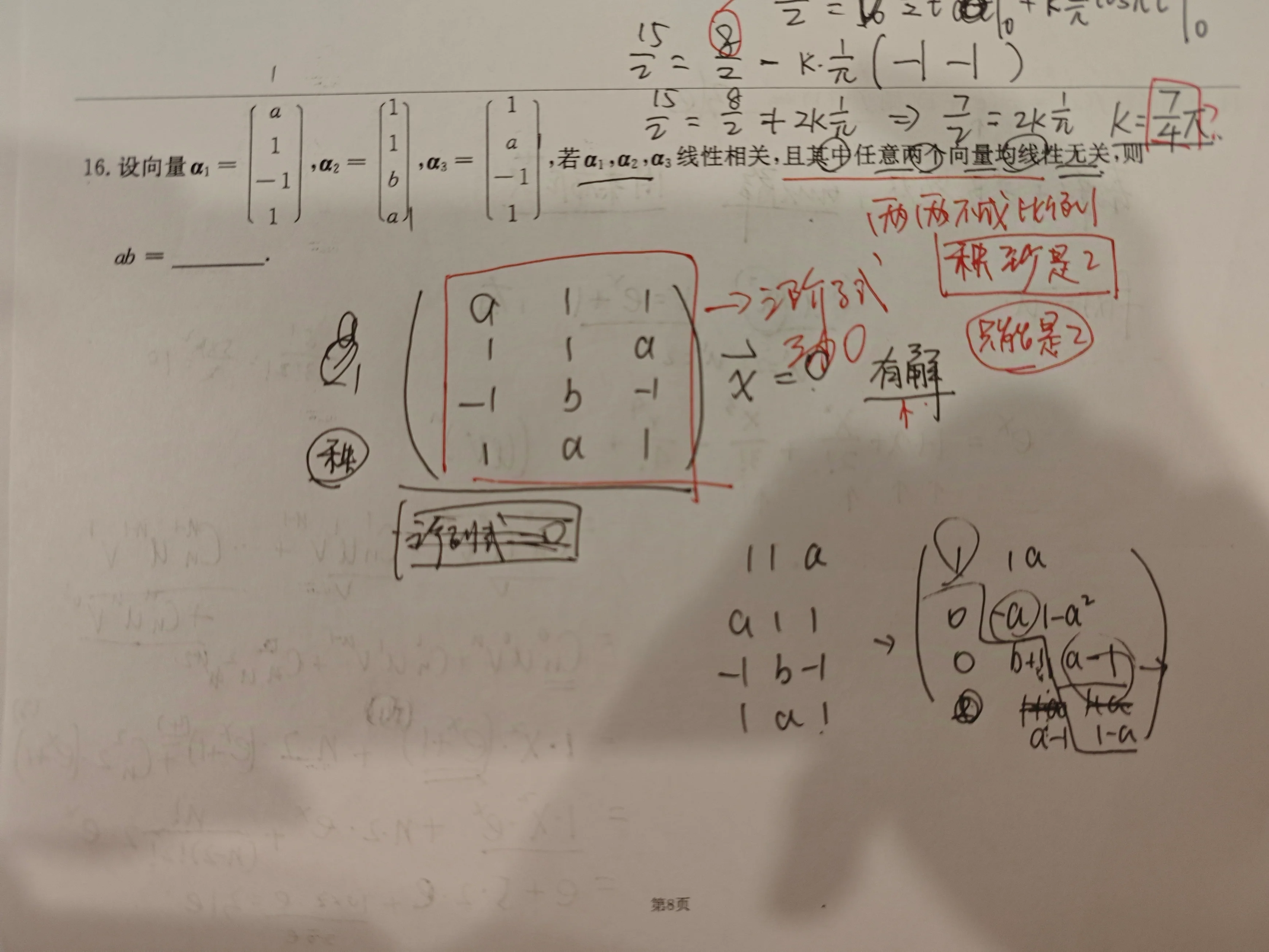
本质上是理解这个秩至少是多少,有一个相似的题目:题3.1
解
[!done]-
由
矩阵的秩 设在矩阵
解) (法一) 由于
由
由此可得
代入
解得
因此,
(法二) 同法一可得
对矩阵
当
当
由此可得
当
由
因此,
[!error]+
设向量
[!NOTE]+
矩阵里面两行两列两两不成比例,那么秩至少是2,这是因为这两个不成比例的行列,可以组成一个二阶主子式

本质上是理解这个秩至少是多少,有一个相似的题目:题3.1
[!done]-
由
矩阵的秩 设在矩阵
解) (法一) 由于
由
由此可得
代入
解得
因此,
(法二) 同法一可得
对矩阵
当
当
由此可得
当
由
因此,