分块查找把查找表分为若干块,每一块记录的数量可以不一样,记录的关键字也可以是无序的,但是块与块之间必须按照关键字大小有序排列,前一块中的最大关键字必须小于后一块中最小的关键字。
分块查找需要建立一个索引表,索引表中的每个元素由各块的最大关键字和该块中关键字的总数构成,索引表中的元素按关键字有序排列。具体查找过程如下:
- 在索引表中确定待查找关键字所在的块,其中的查找算法可以选择顺序查找或折半查找。
- 在选定的块内顺序查找指定的关键字。
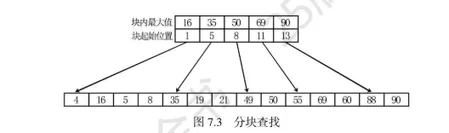
下面给出一个例子,具体说明分块查找的数据组织形式。如图7.3所示(用链表实现以支持动态变化)已知如下14个数据元素的查找表:(4,16,5,8,35,19,21,49,50,55,69,60,88,90),按照关键字16,35,50,69,90将此数组分成5块。
上部分为索引表,索引表中第一行为每一块的最大关键字,第二行为每一块的起始位置,此图中位置标号的起始值为1。
下部分为查找表,在某一个确定的块中使用顺序查找的方式查找关键字。
在图7.3所示表中查找关键字49的具体过程如下:
首先顺序查找索引表(索引表是有序的,因此在索引表中可以使用折半查找),49 > 16,不在第1块,继续比较第2块,49 > 35,不在第2块,继续比较第3块,49 < 50,则如果关键字存在就在第3块,读取该块的起始位置,比较该块的第1个关键字49,查找成功(若比较完该块都没有找到该关键字,不会继续查找下一块,查找失败)。
在此次查找过程中查找索引表比较次数为3次,块内查找比较次数为1次,找长度为1 + 3 = 4。
分块查找的平均查找长度由查找索引表的长度L1和块内查找的长度L2共同决定。现有一个长度为n的查找表,将其以每块大小为j的方式平均分为i块。如果在索引表和块内都使用顺序查找且查找概率相等的情况下,查找索引表的查找长度为: