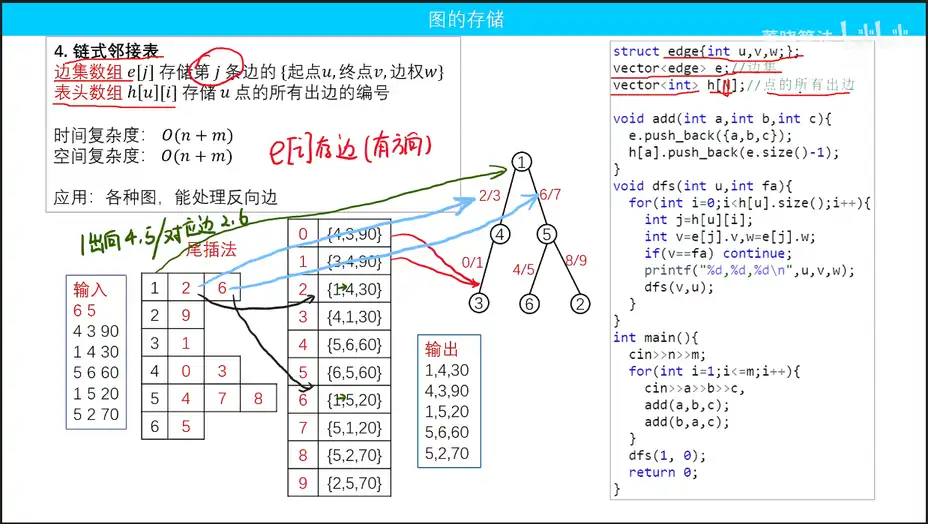
注意这里和邻接表的边集数组做比较,这里的边集数组是一维的,邻接表的边集数组是二维的,要存储每个点的出点
链式邻接表这里的边集数组存储的是每一条边
表头数组看图,存储的是边集数组的下标,也就是每个点连接了哪些边
这是一个二维数组,两个维度是:
- 有哪些点
- 每个点有哪些边
链式邻接表的复杂度
- 时间复杂度
- 空间复杂度
链式邻接表的使用场景
各种图能处理反向边
但是实现比较复杂
链式邻接表的实现
建图
定义数据结构
struct edge{int u,v,w;};
vector<edge> e;
vector<int> h[N];添加边
void add(int a, int b, int c) {
e.push_back({a,b,c}); //添加点
h[a].push_back(e.size()-1); //当前点是在e_i下标下的,推送下标进入这个点
}读取数据
int main() {
cin >> n >> m;
for(int i = 1; i<=m; i++) {
cin >> a >>b >> c,
add(a,b,c); //因为存的是边,所以边的方向不同是不同的东西
add(b,a,c);//这里和邻接表是一样的,都是存两遍
}
dfs(1,0); //1是终点,0是起点,1没有根节点初始化为0
}遍历
搜索点,因为一条边存了两个点,所以遍历的时候要和父节点比对,确认是否来过
void dfs(int u,int fa) {
for(int i = 0 ; i < h[u].size(); i++) { //遍历每个点的邻边
int j = h[u][i]; //拿到这个边
//访问边集数组,从边拿到出去的点和边权
v=e[j].v,w=e[j].w;
if(v==fa) continue;
cout << u << v << w;
dfs(v,u);
}
}