题15
题目
[!question]+
已知函数
(I) 求
(II) 若当
分析
[!NOTE]+
关键还是因式分解
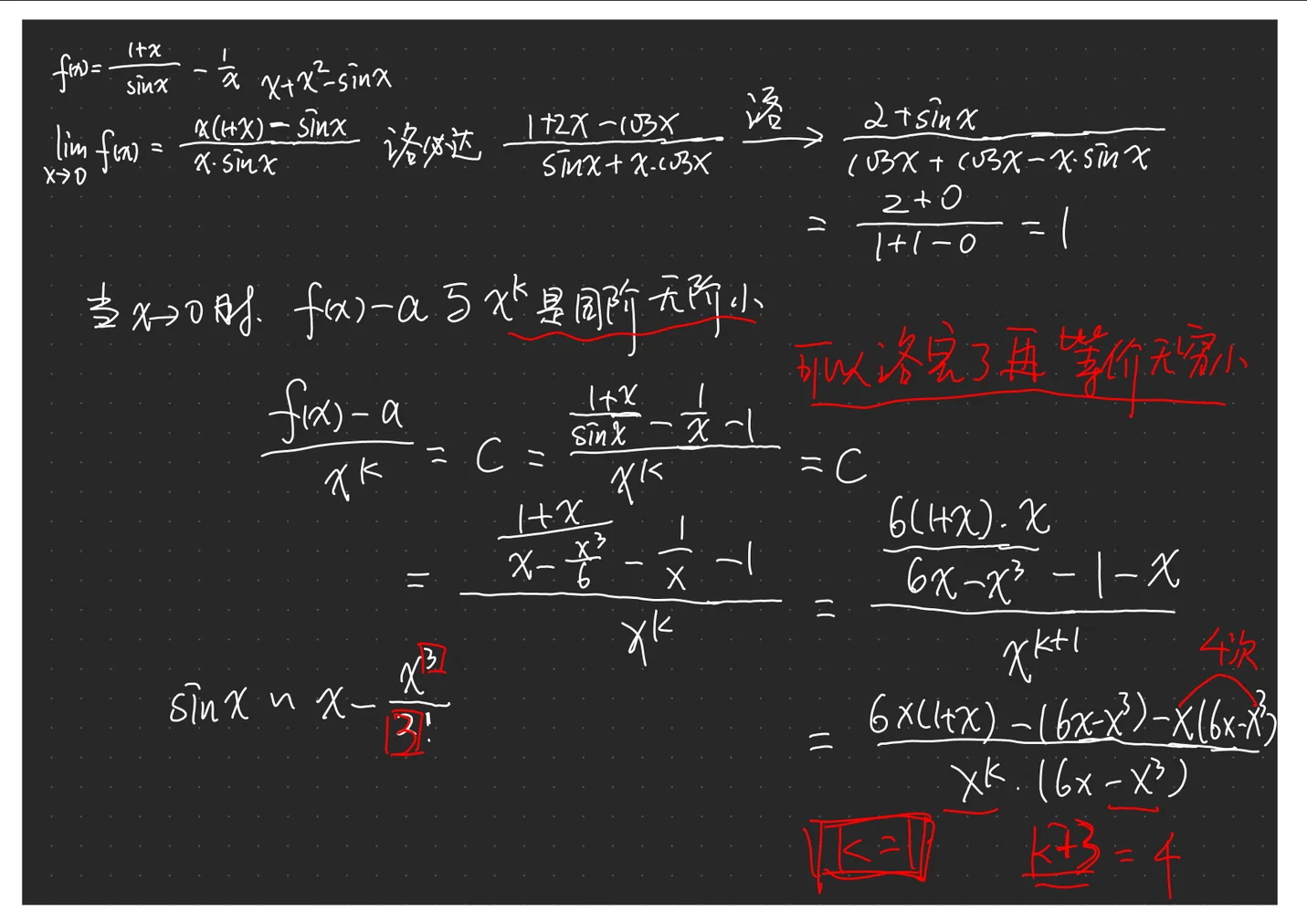
解
[!done]-
解 (I)
考虑
或者,利用
因此,
( II ) 由第( I ) 问得,
若
下面用两种方法来求上面的极限.
(法一) 利用洛必达法则.
要使上面的极限等于非零常数
(法二) 利用等价无穷小替换.
若
因此,
Jun 19, 20254 min read
[!question]+
已知函数
(I) 求
(II) 若当
[!NOTE]+
关键还是因式分解

[!done]-
解 (I)
考虑
或者,利用
因此,
( II ) 由第( I ) 问得,
若
下面用两种方法来求上面的极限.
(法一) 利用洛必达法则.
要使上面的极限等于非零常数
(法二) 利用等价无穷小替换.
若
因此,