多元函数的极限

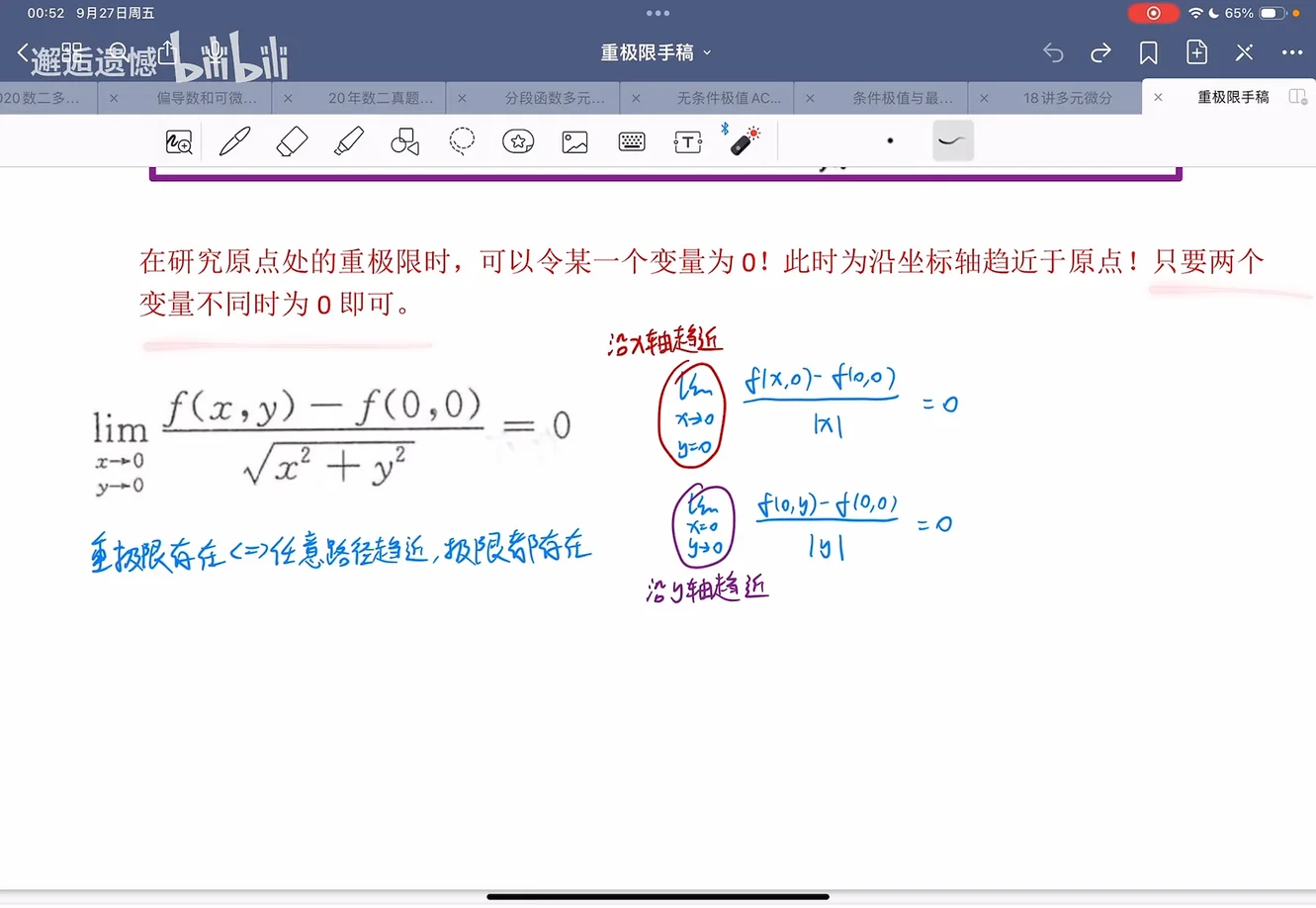
邂逅遗憾说在研究原点处的重极限时，可以令某一个变量为 0! 此时为沿坐标轴趋近于原点!只要两个变量不同时为 0 即可。

分析

A:邂逅遗憾强调的多元函数的极限的问题，累次极限先算内层的东西，内层不存在，整体一定不存在，和重极限区分开来
对于 ,先固定 (视为常数),计算 ,若不存在,则累次不存在; 若存在,再计算 ,若不存在,则累次不存在,若存在,则累次存在.
这里的在0附近有振荡间断点，所以不存在

Link to original

page=171
关于二元函数的极限，有两种定义.下面第一种定义是大部分数学分析教材从点集角度出发的；第二种定义是大部分高等数学教材从邻域角度出发的

第一种定义：
定义 1 设二元函数 的定义域为 ， 是 的聚点 如果存在常数 ，对于任意定的正数 ，存在正数 ，使得当点 时，需有 成立，称常数 为函数 当 时的极限，记作
或
以上是按集合论知识（以点集趋向方式）定义多元函数的极限，通俗说来，只要 是“有定义的”，且满足 ，则，这里自然“排除”了邻域内的无定义点，所以

第二种定义，也就是重极限和任意路径的问题：
若二元函数 在 的去心邻域内有定义，且 以任意方式趋向于 时， 均趋向于 ，则

对于多元函数求极限本质是两次求一元函数的极限，我们称为求累次极限，而最后一个是求二元函数的极限，我们称为求二重极限
page=77