例2.30
题目
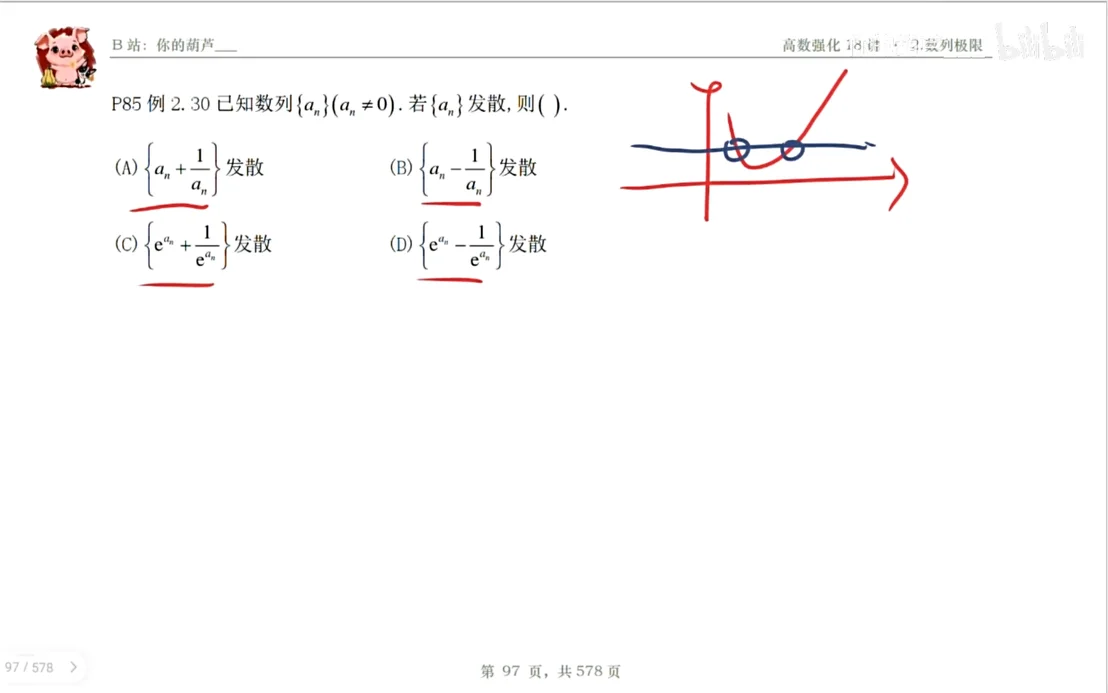
Q:P85 已知数列
(A)
(B)
(C)
(D)
分析
A:这是24年的数二真题
判定函数和数列之间,是不是一一对应的关系,这和例2.29里,那个sin的逻辑是一样的,就是函数本身对应多个自变量,这里的自变量也就是
01:31
当数列
纵轴,函数y的取值的和数列
和2012年数一数二的真题、2017年数二真题,2024年数二真题是一个考法

注意这里可以取逆否命题来简化问题,大前提是,如果函数

解

应选(D).
对于(D),令
【注】至于反例,对于 (A),取
对于 (B),取
对于
事实上, 若不知此题考查的是复合函数极限的定理二, 考场上不一定举得出反例. 现在考研中的选择题, 一定要盯住目标, 明确任务, 而不能总想碰运气, 想排除法.