例3.21
题目
Q:P64 设
(1) 求可逆矩阵
(2) 是否存在 3 阶矩阵
分析
A:关键是把矩阵方程写成多个线性方程组的形式,其中一个齐次线性方程组,两个非齐次线性方程组
1. 求解
这个方程代表的是寻找矩阵
- 首先,我们将
写成矩阵形式:
- 通过观察矩阵
- 从第二个等式,我们得到
- 因此,
为了方便, 我们选择
2. 求解
- 将已知的
- 这等价于求解以下方程组:
- 从第二个等式,我们得到
- 因此,
为了方便, 我们选择
3. 求解
- 类似地,将已知的
- 这等价于求解以下方程组:
- 从第二个等式,我们得到
- 因此,
为了方便,我们选择
解
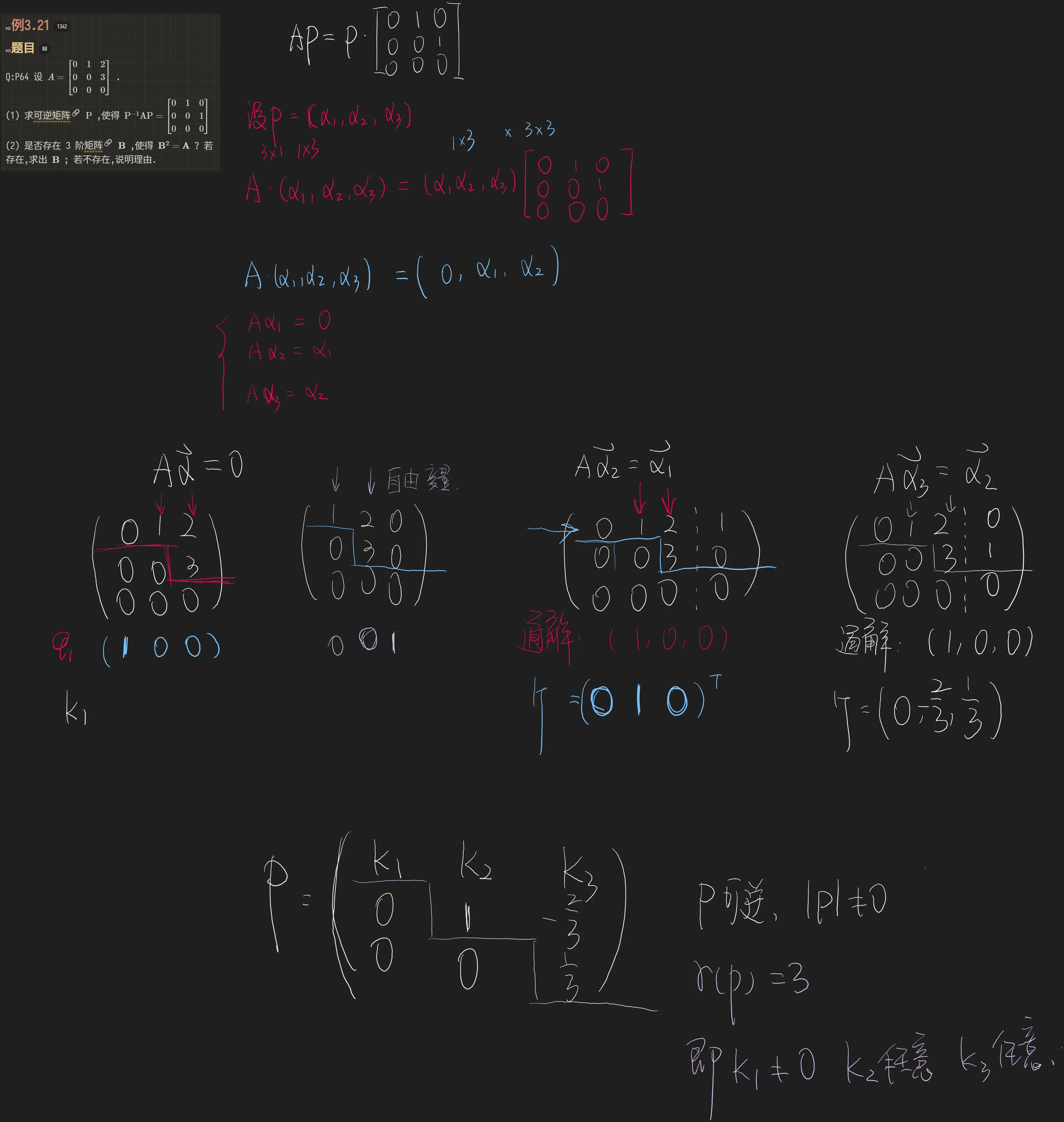
【解】(1) 令
解方程组
解方程组
解方程组
故
( 2 ) 若存在
即
整理得
令各元素对应相等, 故
由
由