题17

题17

题目

[!question]+
设平面有界区域位于第一象限,由曲线与直线围成,计算

分析

[!NOTE]+
用雅可比行列式积二重积分之前，也不妨碍先画出来图看看，尤其这里x和y是符号相反，同时，区域对称性很强，应该先用轮换对称性简化二重积分，我做错了就是因为在无脑算,这是第一个题，不会那么麻烦的

解

[!done]-
解区域如图(a)所示，注意到区域的四条边界曲线中，交换曲线与中的位置，可得与，即曲线方程不变，故这两条曲线均关于直线对称，而直线与直线关于直线对称，故这四条曲线所围成的区域也关于直线对称，从而对变量具有轮换对称性。

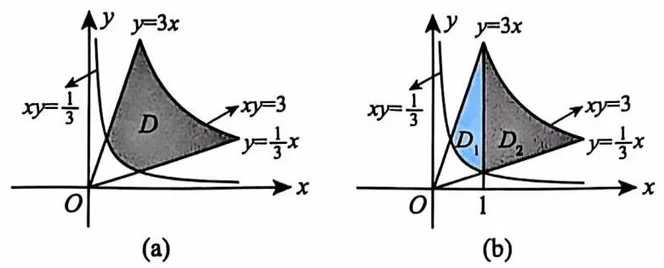
由轮换对称性的结论(2)可得，故

下面用两种方法计算。

(法一)在极坐标系下计算。

曲线的极坐标方程为，整理可得，曲线的极坐标方程为，整理可得。直线的极坐标方程为，的极坐标方程为。区域的极坐标表示为

于是，

由于，故。

当时，，当时，。因此，

(法二)在直角坐标系下计算。

联立解得联立解得联立解得联立

解得

如图(b)所示，直线将区域分为两部分。由曲线，直线与围成，由曲线，直线与围成，等于的面积，即的面积与的面积之和。因此，

注：与本题中的区域类似的区域在2015年的真题中出现过，只不过是一道选择题，题目仅要求将区域表示转化为极坐标形式，写出极坐标形式下的积分即可，而本题需要将积分计算出来。

【例】设是第一象限中由曲线与直线围成的平面区域，函数在上连续，则 ( )(2015年数学一、二试题)

(A) . (B) .

(C) . (D) .

答案 B.