题4

题4

题目

[!question]+
设函数 在 内连续,其导函数的图形如图所示, 则( )

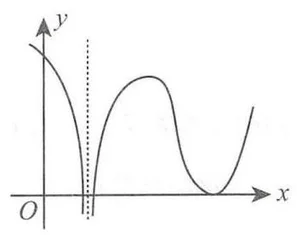
(A) 函数 有 2 个极值点,曲线 有 2 个拐点.
(B) 函数 有 2 个极值点,曲线 有 3 个拐点.
(C) 函数 有 3 个极值点,曲线 有 1 个拐点.
(D) 函数 有 3 个极值点,曲线 有 2 个拐点.

分析

[!NOTE]+
拐点要注意看一阶导增减性变化的点，也就是也就是一阶导不可导，一阶导的导函数不存在的点，这里就是x2了

解

[!done]-
解 观察图形, 共有 4 个可能的极值点,从左至右依次记为 , ,其中 为虚线与 轴的交点,其余三点为 与 轴的交点. 在 处, ,在 处, 不可导.

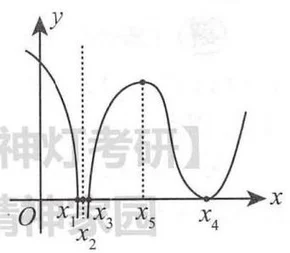
分别考察 左、右小邻域内的 的符号.

• 当 时, ; 当 时, . 故 是 的极大值点.
• 当 时, ; 当 时, . 故 不是 的极值点.
• 当 时, ; 当 时, . 故 是 的极小值点.
• 当 时, ; 当 时, . 故 不是 的极值点.

因此, 共有 2 个极值点.

曲线 的可能的拐点从左至右依次为 ,其中 不存在, .

当 时, 单调减少; 当 时, 单调增加. 故点 是曲线 的拐点.

• 当 时, 单调增加; 当 时, 单调减少. 故点 是曲线 的拐点.

当 时, 单调减少; 当 时, 单调增加. 故点 是曲线 的拐点.

因此,曲线 共有 3 个拐点.

综上所述,应选 B.

注 本题有两个地方容易出错.

① 在判断 的极值点时,只注意到 ,而没有注意到 左、右两侧小邻域内的 均大于零,从而误将 当作极值点.

② 在判断 的拐点时,忽略了 不存在的点,即 ,从而认为只有 2 个拐点.